LIPIEC 2025| LJK | ~2 954 słów |~ 20 597 znaków|
Estymator to po prostu statystyka opisowa. Średnia to estymator. Odchylenie standardowe to estymator. Każda statystyka opisowa, która ma oszacować prawdziwą, populacyjną wartość zmiennej jest jednocześnie estymatorem. Niektóre z nich są lepsze, inne - gorsze. Co decyduje, że sięgamy do średniej jako miary średniego nasilenia zmiennej w populacji? Okazuje się, że jest ona estymatorem o najlepszych własnościach - nieobciążonym, efektywnym i zgodnym. Co znaczą te pojęcia? Wyjaśniam w tym tekście.
Wprowadzenie
1️⃣ Na wszystkie statystyki opisowe, jakie omówiliśmy na tym blogu, np. miary tendencji centralnej KLIK albo miary rozproszenia KLIK, można patrzeć z zupełnie innej strony niż tylko ta, z jakiej poznajemy je najczęściej - ta, w której są tylko narzędziami opisu próby, np. średniego reprezentanta zgromadzonego zbioru danych. Statystyki opisowe to znacznie coś więcej niż tylko liczby podsumowujące próbę. Obok tego, są również liczbami, które pozwalają podglądać to, co dzieje się w populacji - jak przez dziurkę od klucza. Niestety, nie jest to pełny obraz. Nie mając pełnego dostępu do populacji, a tylko do jej części, otrzymujemy tylko przybliżenie tego, co dzieje się naprawdę - jakieś oszacowanie prawdziwych, populacyjnych wartości. Stąd można powiedzieć, że wszystkie statystyki opisowe są jednocześnie statystykami szacującymi.
2️⃣ Aby dobrze zrozumieć tematykę tego posta, musimy pamiętać, że istnieją dwa poziomy organizacji jednostek - próba i populacja, ponieważ podział ten przekłada się na relację między estymatorami, statystykami i parametrami. O populacji mówi się, że to "ogół jednostek, który posiada jakąś własność", np. wzrost, waga itd. i tak się składa, że chcemy tę własność poznać. Liczbowa własność charakteryzująca populację nazywa się parametrem. Próba to część populacji. Statystyki opisowe są obliczane na podstawie próby to parametry, są one własnościami populacji. Parametrem jest np. średni poziom wzrostu w populacji albo odsetek osób palących. Zauważ zmianę w oznaczeniach poziomu organizacji jednostek. Jeśli średni wzrost w populacji wynosi μ = 164.7 cm, to statystyką w próbie jest średnia arytmetyczna x̄ = 165.6 cm obliczona z udziałem, przykładowo, N = 32 zebranych osób.
Wszystkie statystyki opisowe są tzw. estymatorami - narzędziami, które pomagają odkryć prawdziwą wartość w populacji, czyli profesjonalnie mówiąc: oszacować albo estymować. Prawdziwa wartość charakteryzująca populację nazywa się parametrem. Krótko mówiąc, statystyki opisowe estymują parametry populacji.
3️⃣ Jaka jest różnica między statystyką opisową a estymatorem? Na papierze (czyli we wzorach) - żadna. Statystyka opisowa to estymator. Estymator to statystyka opisowa. Mówimy o tym samym narzędziu statystycznym. Natomiast tym, co ulega zmianie, to intencja rozmówcy. Gdy mówi się o średniej jako o statystyce opisowej, skupiamy na opisie próby, miary tendencji centralnej, miary czegoś, co ma być reprezentantem. Gdy mówi się o średniej jako o estymatorze, to skupiamy się na średniej jako narzędziu służącym do szacowania.
Rodzaje estymatorów - punkty i przedziałowy
Są dwa rodzaje estymatorów - punktowy i przedziałowy.
ESTYMATOR PUNKTOWY | to taki, który jest pojedynczą liczbą, np. 5.12 albo -6,06. Przykładem estymatora punktowego jest średnia arytmetyczna. Oprócz średniej arytmetycznej, estymatorem punktowym jest odchylenie standardowe, skośność, kurtoza - praktycznie wszystkie statystyki opisowe, które poznałeś.
ESTYMATOR PRZEDZIAŁOWY | to taki, który rozszerza się na cały przedział liczbowy zawierającym wartości od dolnego krańca do górnego. Często ten przedział zapisuje się za pomocą prostokątnych nawiasów, np. [2.21; 7.76]. Typowym i najczęściej przytaczanym przykładem estymatora przedziałowego jest przedział ufności średniej (ang. confidence interval of mean, CI).
Technicznie rzecz biorąc, estymator przedziałowy składa się z dwóch estymatorów punktowych - jeden jest początkiem tego przedziału, a drugi - jego końcem.
Największa różnica między dwoma rodzajami estymatorów nie leży w budowie, tylko w ich interpretacji. Na przykład, średnia arytmetyczna x̄ może być interpretowana jako typowy egzemplarz w próbie albo środek ciężkości histogramu. Rzadko kiedy ktoś odnosi średnią arytmetyczną obliczoną w próbie bezpośrednio do średniego nasilenia zmiennej w populacji, mówiąc:"na 90% wartość średnia x̄ jest równa średnie μ". Inaczej sprawy mają się z przedziałem ufności średniej, którego interpretacja jest mniej intuicyjna i wbrew powszechnym przekonaniom, przedział ufności nie mówi o pewności, z jaką średnia w populacji zawiera się w obliczonym przedziale μ. Więcej przeczytasz tu:KLIK
➡️ Ale dlaczego średnia jest dobrym narzędziem? Dlaczego możemy wierzyć jej jako oszacowaniu prawdziwej średniej, tej populacyjnej? I tu wracamy do pytania z początku tego posta. We wprowadzeniu zaczęliśmy uprawiać gdybologię stosowaną - co stałoby się, gdybyśmy zebrali inną próbę?
Odpowiedź na pytanie, co to znaczy dobry estymator, jednocześnie pokazuje to, co daje statystyka.
Jak badać zachowanie estymatorów?
Dobroć estymatora bada się na podstawie różnych jego wartości. Ale skąd je wziąć, kiedy badacz dysponuje tylko jedną próbą - jednym badaniem, które zaplanował, zorganizował i przeprowadził? Musiałby przecież powtórzyć to samo badanie, jeszcze raz i jeszcze raz, aby otrzymać wiele różnych wartości tego samego estymatora. Dlatego należy uruchomić wyobraźnię albo symulacje komputerowe - a najlepiej jedno i drugie. Na wykładzie mówię, że stworzymy 100 badaczy, którzy badają to samo zjawisko, gromadzą próbę i obliczają średnią arytmetyczną. Dla ułatwienia nie wyskakuję z jakimiś zagadnieniami typowo psychologicznymi, aby nie odwracać uwagi i zajmuję się jakimś powszechnie występującym zjawiskiem, np. wzrostem i na dodatek w obrębie jednej płci (u kobiet) a spośród estymatorów średnia arytmetyczna staje się przykładem, na podstawie którego poznajemy zachowanie dobrego estymatora.
Na stronie worldonline.pl znalazłam informację, że średni wzrost kobiet w populacji μ = 164.7 cm (populacyjny, dlatego grecka literka μ /mi/).
Ta wartość jest efektem statystycznego modelowania wzrostu kobiet. Nikt nie zbadał wzrostu wszystkich kobiet na planecie, a przynajmniej ja tego nie pamiętam, żeby brała w nim udział. Ten fakt nie przeszkodzi nam w wykorzystaniu tej liczby jako populacyjnego średniego nasilenia zmiennej Wzrost do naszych celów.
Rozkład zmiennej - w jednej próbie i w wielu próbach
🟠 Wyobraźmy sobie, że zmierzyliśmy wzrost N = 5 kobiet. Oto wyniki pomiaru 158.77, 160.25, 166.00, 167.04, 176.03. Przedstawione na wykresie histogramu wyglądają tak, jak na grafice po prawej stronie. Ich średnia wynosi x̄ = 165.2.
Do lepszej obserwacji tego, co będzie się dalej działo, wygodniej będzie przypomnieć sobie jedną z właściwości histogramu. Sam wykres pokazuje ile obserwacji przytrafiło się w konkretnym przedziale liczbowym. Jeśli wycięlibyśmy jego kształt ze sztywnego kartonu i następnie ustawili go na czymś, co może służyć za podparcie - palec, kij, długopis albo inny walcowaty przedmiot - odkrylibyśmy, że punkt równowagi wyciętego z kartonu histogramu znajduje się w tym miejscu na osi poziomej OX, gdzie leży średnia arytmetyczna próby, x̄. Punkt równowagi jest zaznaczony na rysunku pomarańczowym trójkątem 🛆. To jedna z kilku interpretacji średniej arytmetycznej jako środka ciężkości histogramu, która ułatwi nam obserwowanie zachowania histogramów.
Wróćmy teraz do naszej pięcioelementowej próby. Nie dziwi nas ani to, że średnia w próbie wynosi x̄ = 165.62 cm zamiast 164.7 cm, ani również to, że histogram wcale nie przypomina rozkładu normalnego. Trudno byłoby go wcisnąć w foremkę dzwonu Gaussa. Dlaczego tak dzieje się? Dlatego, że pięcioelementowa próba jest bardzo małym podglądem na populację. Każda z pięciu obserwacji wywiera duży wpływ na statystyki opisowe czy wygląd wykresów.
📌 Właśnie dlatego potrzeba nam odpowiedź na to, czy średnia jest dobrą miarą położenia próby, czy to, z jaką próbą mamy do czynienia nie wywiera za dużego wpływu.
🟠 Wyobraźmy sobie teraz, że każdy ze stu badaczy przebadał tylko pięć kobiet (łącznie to 100 · 5 = 500 kobiet, tyle, że rozdzielonych po pięć między stoma badaczami). Jak mogłyby wyglądać histogramy wzrostu? Na rysunku przedstawię tylko 50 pierwszych histogramów zmiennej Wzrost, bo umieszczenie wszystkich pięciuset na jednym rysunku jest kłopotliwe. Wystarczy nam część, aby wyciągnąć ważny wniosek.
 |
| Rys. 50 histogramów tej samej zmiennej w różnych próbach o tej samej liczebności |
Oto grafika przedstawiająca wiele histogramów tej samej zmiennej (tj. Wzrostu) w różnych próbach o tej samej liczebności. Wprawdzie mają tę samą liczebność kobiet (n = 5 każda), ale zawierają różne obserwacje (mierzono przecież różne kobiety). To jest powód, dla którego histogramy różnią się. Każdy z badaczy ma po prostu inną piątkę kobiet. Po drugie nie dość, że mamy do czynienia ze zmiennością między próbami, to jeszcze ze zmiennością między średnimi. Ilustruje to fakt, że średnia arytmetyczna każdej z piątek ani nie wynosi 164.7 (już wiemy dlaczego), ale na dodatek w każdej z prób jest inna.
Dlaczego niektóre histogramy są identyczne? Można byłoby pomyśleć, że identyczność histogramów oznacza identyczność prób - że są to te same osoby. Byłaby to jednak duża pomyłka. Identyczność histogramów wynika z tego, że owszem próby są zbliżone, ale algorytm, który tworzy te histogramy, tak po prostu podzielił zakres wartości próby na przedziały, zwane kubełkami, a potem zliczył ich zawartość - i pokazał się ten sam kształt histogramu. Więcej o histogramie przeczytasz tu: KLIK.
🟠 Na histogramie czerwona kropka na osi OX oznacza średnią arytmetyczną w danej próbie. Przyjrzyj się i zobacz, że nie stoi ona w miejscu. Dla różnych histogramów stoi w różnych miejscach. Sygnalizuje to, że średnia zmiennej różni się w zależności od próby z jaką mamy do czynienia. To zupełnie normalne zjawisko.
Rozkład średnich (zmiennej) z próby - próbkowy rozkład statystyki opisowej
Aby zagłębić się w teorię estymatorów, zaczniemy od wejścia w temat powoli, po kostki, kontynuując przykład ze stoma badaniami Wzrostu, w którym każde liczy 5 kobiet. Dla ułatwienia kolory rysunków zmienią się. O ile niebieski kolor oznaczał histogram zmiennej, o tyle brązowy kolor histogramu będzie oznaczać zupełnie inną rzecz.
🔵 Zauważ, że jeśli dysponujemy sto średnich obliczonych na próbach liczących po pięć kobiet każda, powstaje sto liczb - sto średnich - dla których możemy wykreślić kolejny histogram. Tym razem będzie to histogram nie samej zmiennej (tu: Wzrostu kobiet), a histogram statystyki opisowej (tu: średnich zmiennej Wzrost).
 |
| Rys. Próbkowy rozkład średniej - czyli rozkład wielu średnich z prób o tej samej liczebności. |
Ten histogram już nie zmiennej, a wybranej statystyki opisowej, moglibyśmy nazwać metahistogramem od greckiego przedrostka meta oznaczającego poza. Taka nazwa odróżniałaby zwykłe histogramy, takich które opisują próbę, od histogramów nieco bardziej abstrakcyjnych, które pokazują "co by było, gdybyśmy coś zrobili". Niestety, zamiast krótkiej nazwy, jest inna, znacznie dłuższa.
🔵 Ten rozkład nazywa się próbkowym rozkładem średniej (ang. sampling distribution of mean) albo rozkładem z próby. Słowo próbkowy oznacza, że ten rozkład nie opisuje wartości badanej zmiennej w próbie, ale wartości średniej (raczej: wielu średnich) w wielu próbach.
Gwoli ścisłości - ten histogram jest tzw. empirycznym próbkowym rozkładem średniej, ponieważ został zbudowany jedynie na stu średnich, a nie na wszystkich możliwych pięcioelementowych próbach złożonych z pięciu kobiet. Na świecie jest dużo więcej kobiet niż 500.
ROZKŁAD Z PRÓBY. ROZKŁAD W PRÓBIE. ROZKŁAD W POPULACJI | W statystyce mamy dwa określenia na rozkłady dwóch różnych rzeczy, które różnią się jedną literą: rozkład w próbie to rozkład wartości badanej zmiennej, np. Wzrostu, jakie udało się zmierzyć w zgromadzonej w próbie. Ten typ rozkładu (tj. w próbie) możemy bezpośrednio zbadać, rysując wykres słupkowy albo histogram (w zależności od skali pomiarowej badanej zmiennej). Rozkład zmiennej z próby to rozkład zupełnie czegoś innego. Jest to rozkład statystyki opisowej, a nie wartości zmiennej. To twór teoretyczny, który pokazuje jakich wartości statystyki opisowej, np. średniej, możemy spodziewać się, gdybyśmy przeprowadzili nie jedno badanie, a wiele takich samych. Do narysowania wykresu tego rozkładu jedna próba nie wystarczy. Ten rozkład można częściowo zasymulować za pomocą symulacji komputerowych albo wydedukować za pomocą matematycznych narzędzi. Czy któryś z nich odpowiada rozkładowi cechy w populacji? Nie. Rozkład cechy w populacji nosi pełną nazwę "rozkładu cechy w populacji".
🔵 Przyjrzymy się teraz temu histogramowi. Gdy średnie są liczone na pięciu osobach każda, to widząc je zagregowanymi na histogramie trudno nie zauważyć, że rozrzut jest dość duży, wynosząc 171.65 - 157.40 = 14.25. Badacz może otrzymać średnią równą 157,40, ale też równą 171,65. Punkt ciężkości tego histogramu leży w 164.49. Moglibyśmy powiedzieć, że średnia średnich x̄x̄ w tym przypadku właśnie tyle wyniosła, choć tworzymy wówczas pojęciowego potworka, którego zwykle staram się unikać na wykładzie 🫤. Zakres rozrzutu sugeruje, że zmienność średnich z próby na próbę jest duża. W takim razie gdzie ta wiara pokładana w średniej arytmetycznej? Spokojnie, małe próby charakteryzują się dużym udziałem czynników losowych, które kreują daną próbę, a co za tym idzie wartości statystyk opisowych. Magia zaczynie się dziać, gdy zwiększymy liczbę osób badanych.
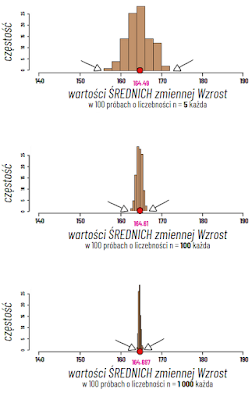
➡️ Wykreślmy histogramy średnich w stu badaniach, ale dla zwiększającej się liczby kobiet. Twoim zadaniem jest przyglądać się trzem rzeczom - rozpiętości histogramu na osi OX, temu, gdzie znajduje się czerwona kropka symbolizująca średnią arytmetyczną i kształtowi tego histogramu. Obserwując zachowanie tych histogramów, omówimy trzy własności dobrego estymatora na podstawie średniej arytmetycznej x̄.
Widzimy, że histogramy robią się coraz węższe. Tym razem nie jest to efekt manipulacji podziałką na osi poziomej OX, ponieważ nie zmienia się, zaczynając na wartości 140 a kończąc na 190. Ostatni histogram to histogram średnich, jakie można otrzymać prowadząc badania na 1 000 osób, gdzie histogram jest bardzo wąski. Teraz możemy wreszcie przedstawić podstawowe własności dobrego estymatora.
Cechy dobrego estymatora
1️⃣ Warto zauważyć, że na każdym z histogramów czerwona kropka znajduje się blisko teoretycznej wartości μ = 164,7 cm - i tak nawiązujemy do pierwszej własności estymatorów - nieobciążoności (ang. unbiasedness). Teoria estymatorów mówi, że niezależnie od wielkości próby czerwona kropka powinna znajdować się w miejscu teoretycznej wartości średniej.
🤔 Dlaczego tutaj średnia jest nieznacznie przesunięta raz w jedną, raz w drugą stronę? Wyjaśnienie tego fenomenu w zasadzie padło już wcześniej. Histogramy średnich, jakie oglądasz, to tzw. empiryczne histogramy, które zostały stworzone tylko dla stu prób o pięciu elementach. Niestety, nie wyczerpują one całej puli wszystkich pięcioelementowych prób. Gdybyśmy przebadali wszystkie możliwe próby o n = 5 obserwacjach, a nie tylko ich część, zobaczylibyśmy dwie rzeczy: (a) zamiast histogramów pojawiłaby się gładka, ciągła linia reprezentująca rozkład już nie empiryczny, a teoretyczny (profesjonalnie nazywa się gęstością); (b) środek ciężkości takiego rozkładu teoretycznego znajdowałby się dokładnie nad wartością 164.7 cm. Tu nie widzimy tego tak dokładnie, ponieważ dysponujemy tylko częścią prób wygenerowanych za pomocą symulacji komputerowych, a nie wszystkimi.
Używając pełnych nazw, można powiedzieć, że nieobciążoność średniej arytmetycznej jako estymatora oznacza, że średnia rozkładu próbkowego średniej arytmetycznej jest równa średniej populacyjnej badanej zmiennej.
Nieobciążoność jest odpowiedzią na pytanie o to, co dzieje się ze średnimi w obrębie wielu badań o tej samej strukturze (tak samo obliczona samoocena, w grupach o tej samej liczebności). Nieobciążoność mówi, że gdybyśmy mieli wszystkie próbki tej samej wielkości, to rozkład średnich ma szczyt położony nad populacyjną wartością, 164.7.
Co nam daje ta abstrakcyjna wiedza, że jakiś superteoretyczny rozkład o dziwnej nazwie ma szczyt położony dokładnie nad prawdziwą wartością z populacji? Ważną informację o tym, czy narzędzie, którym posługujemy się do szacowania własności populacji, jakiej nie możemy bezpośrednio zbadać, nie popełnia niepotrzebnych błędów wynikających z jego budowy tzw. błędów systematycznych. Nieobciążony estymator sam z siebie nie dodaje i nie odejmuje od szacowanej wartości. Za wszelkie rozbieżności między jego wynikiem a prawdziwą populacyjną wartością odpowiadają losowe wahania w próbie.
W przeciwieństwie do estymatorów nieobciążonych, estymatory obciążone popełniają błędy, które nie wynikają z tego, że ktoś się zagapił, albo przejeżdżał tramwaj i budynek drgał a drgania przeniosły się na aparaturę. Ich obciążenie jest obciążeniem systematycznym, stałym, pojawiającym się w każdej próbie. Działanie obciążonego estymatora można porównać do działania popsutej waga, która dodaje kilogramy.
Słowa używane w statystyce mają nieco inne znaczenie niż te używane na co dzień. Obciążenie kojarzy się nam z nadmiarem, tymczasem statystyczne obciążenie to w ogóle nietrafność - albo niedoszacowania albo przeszacowania.
Omówiliśmy zachowanie czerwonej kropki. Pora na zachowanie histogramu wzdłuż poziomej osi OY.
2️⃣ Rozrzut histogramu średnich, gdy badano pięcioelementowe próby wyniósł 14.25, ale na kolejnych rysunkach jest on coraz mniejszy tak, że na ostatnim wynosi 1.23. Śledząc zakres histogramów, obserwujemy, że wraz ze wzrostem liczebności w próbach histogramy robią się coraz węższe i węższe. Rozrzut różnych wartości średniej arytmetycznej, jaki mogą otrzymać badacze, zmniejsza się. Im większa próba, tym bardziej zbliżone do siebie wyniki. To wspaniała wiadomość, zgodna z intuicją. Przecież im więcej osób przebadałby każdy z badaczy, tym bardziej zbliżone do siebie otrzymaliby średnie arytmetyczne.
Ta własność nazywa się efektywnością estymatora(ang. efficiency) albo jego minimalną wariancją (ang. minimal variance).
Gwoli ścisłości, aby w pełni pokazać tę własność trzeba byłoby zestawić średnią z jakąś inną miarą i pokazać, że w przypadku średniej arytmetycznej ten rozrzut jest najmniejszy z możliwych.
Z tym zjawiskiem związane jest pojęcie tzw. błędu standardowego (ang. standard error of mean). Błąd standardowy średniej to odchylenie standardowe w rozkładzie średnich. Mówi nam o tym, jak dobrze sprawuje się średnia x̄ jako estymator prawdziwego średniego nasilenia zmiennej w populacji μ. I nic dziwnego w tym, że wraz ze wzrostem próby, błąd standardowy zmniejsza się. Co prawda na tych rysunkach lepiej widoczny jest rozrzut, ale nie przeszkadza to.
Spójrzmy teraz na te same wykresy, ale tym razem całościowo na kształt histogramów - nie tylko na zakres.
3️⃣ Obserwując trzy rysunki po prawej stronie widzimy, że kształt histogramów średnich staje się coraz bardziej koncentrowany wokół teoretycznej wartości μ. Ramiona histogramów opadają ku osi OX, a szczyt coraz bardziej wypiętrza się ku górze. To zjawisko nazywa się zgodnością (ang. consistency).
Zgodność to praktyczna własność, którą można wymyślić samemu. Oznacza ona, że wraz ze wzrostem liczby osób badanych, średnia pojedynczej próby coraz bliżej leży prawdziwej, populacyjnej średniej μ = 164.7 cm.
Można odnieść wrażenie, że nieobciążoność i zgodność to to samo. A jednak nie. Nieobciążoność mówi o tym, co dzieje się ze środkiem ciężkości histogramu średnich. Zgodność mówi o tym, że kształt histogramu robi się coraz bardziej skoncentrowany nad tym środkiem ciężkości.
🏁 PODSUMOWANIE | Kilka informacji o własnościach estymatorów do zapamiętania:
➡️ Estymator i statystyka opisowa to dwie strony tego samego medalu, tego samego narzędzia statystycznego. Kiedy narzędzie podsumowuje jakiś aspekt próby, wówczas występuje w roli statystyki opisowej a kiedy zastanawiamy się, czy dobrze szacuje wartość w populacji, to - w roli estymatora.
➡️ Co stałoby się, gdybyśmy przeprowadzili to samo badanie jeszcze raz i jeszcze raz, za każdym razem licząc tę samą statystykę opisową? - od tego pytania warto zacząć. Czy wartości tej statystyki opisowej byłyby takie same? Różne? Czy koncentrowałyby się wokół jakiejś wartości?
➡️ Różne wartości statystyki opisowej w różnych próbach tworzą tzw. rozkład próbkowy (ang. sampling distribution). Na jego podstawie można wywnioskować to, czy dana statystyka opisowa dobrze pełni rolę estymatora.
➡️ Są trzy cechy dobrego estymatora: po pierwsze ma sam z siebie niczego nie dorzucać, po drugie - jego wartości mają niewiele różnić się między próbami; po trzecie - ma być coraz bliższy wartości w populacji wraz z rosnącą liczbą obserwacji w próbie. Te trzy cechy noszą nazwy (odpowiednio): nieobciążoność, efektywność (zwana też minimalną wariancją) i zgodność.





3 komentarze:
Ekstra!
Bardzo dziękuję :-) pozdrowienia!
Bardzo zrozumiale wytłumaczone
Prześlij komentarz