Diagnostyka normalności: Liczby i rysunki

Rozkład normalny to podstawowy rozkład w statystyce. Mówimy, że taka-to-a-taka cecha ma rozkład normalny. Że założenia testów różnych testów statystycznych: testu t-Studenta oraz analizy wariancji ANOVA wymagają rozkładu normalnego. Że model jest dobry, gdy rozkład błędów jest normalny. Skąd jednak badacz ma wiedzieć, czy zebrane przez niego liczbowe wartości zmiennej układają się zgodnie z krzywą Gaussa? W tym poście piszę, jak należy sprawdzać, czy cecha w zebranej przez Ciebie próbie może mieć rozkład zbliżony do normalnego. Jeśli chcesz przejść od razu do narzędzi, kliknij tutaj: KLIK.

SPIS TREŚCI: Diagnostyka normalności a typ pomiaru: czy każdą zmienną można badać pod katem normalności? Czy istnieje jeden rozkład normalny: na czym polega ocena normalności rozkładu? Pięć narzędzi diagnostycznych i omówienie ich zachowania w populacji (teoretyczne wartości) Narzędzia diagnostyczne: ich zachowanie w próbie [TU JEST TO, CZEGO SZUKASZ] Czy testy normalności koniecznie trzeba stosować? DIY - Diagnostyka normalności w SPSS

WPROWADZENIE — W każdej dziedzinie jest zbiór pojęć rozpoznawanych poza nią. W psychologii jest to np. procesy poznawcze. W statystyce takim pojęciem funkcjonującym w zbiorowej świadomości jest rozkład normalny łatwo zapamiętywalny ze względu na charakterystyczny, dzwonowaty kształt. Wiele lat temu uważano, że rozkład normalny stanowił dobry model zjawisk społecznych. Obecnie odchodzi się od tego myślenia, ale nie zmienia to jego popularności, zwłaszcza że analizy, jakie wykorzystują badacze, opierają się na tym rozkładzie. Więcej informacji na temat rozkładu normalnego znajdziesz w poście  KLIK. Tutaj ograniczymy się do tylko części potrzebnej do zrozumienia, jak działają narzędzia diagnostyczne służące do - jak sama wskazuje - diagnozy tego, czy badana cecha ma rozkład normalny. Takie zadanie często stoi przed badaczem i najprawdopodobniej szukałby on jakiegoś testu statystycznego. Wiadmo, jak statystyka, to testy. Badacze mają nawyk testowania wszystkiego w dobrym i złym tego słowa znaczeniu, więc nic dziwnego, że jako pierwsze przychodzą do głowy testy statystyczne. Istnieją jednak inne nie-testowe metody oceny normalności rozkładu — i o tym jest ten post.

DIAGNOSTYKA NORMALNOŚCI A TYP POMIARU — Narzędzia służące do oceny normalności rozkładu stosujemy tylko i wyłącznie wtedy, gdy wiemy, że mierzona przez nas zmienna czy badana cecha ma najwyższy w skali Stevensa, ilościowy typ pomiaru, np. jest to czas reakcji, wiek, długość, szerokość. Często przyjmuje się, że wyniki ogólne w kwestionariuszach również charakteryzują się tym typem pomiaru. Chodzi o to, że narzędzia, jakie zaraz poznasz, działają dla tych zmiennych, których wartości reprezentują matematycznie rozumiane liczby. Liczby, które można dodawać, mnożyć, dzielić, a nie "liczby" ujęte w cudzysłów, bardziej znaki graficzne, jak dla zmiennej nominalnej albo porządek jak dla zmiennej porządkowej. Rozkład normalny mogą posiadać jedynie zmienne ilościowe. Nie badamy normalności dla płci (kobieta, mężczyzna, niebinarna) czy wykształcenia (mierzonego kategoriami: podstawowe, średnie, wyższe)

CZY ISTNIEJE JEDEN ROZKŁAD NORMALNY? Patrząc na powyższy rysunek, widzimy tylko jeden z możliwych rozkładów normalnych. Taki, który ma parametry 0 i 1. Kreskowaną linią zaznaczono szczyt tej krzywej, który jednocześnie jest średnią. Ponieważ zamiast zera i jedynki może stać tutaj absolutnie dowolna liczba rzeczywista, to rozkładów, o których można powiedzieć, że są normalne, jest nieskończenie wiele. Dlaczego jest ich nieskończenie wiele, a jakby jeden? Wszystkie łączy ten sam wzór ogólny. Posiadając wspólną matematyczną formułę, tworzą jedną rodzinę. Jedyne, co się w niej zmienia, to drobiazgi zwane parametrami - to co na rysunku jest zerem i jedynką. Ogólny wzór pozwala narysować krzywą Gaussa przypominającą dzwon (choć czasem trudno go zobaczyć).

Na podobnej zasadzie działa funkcja liniowa np. y = x + 2 lub y = -x - 1.

W każdym wzorze zamiast jedynek i dwójek mogłaby stać dowolna inna liczba, a i tak nadal byłaby to funkcja liniowa z wykresem w postaci linii prostej. Wszystkie spełniają tzw. ogólny wzór postaci: y = a*x+b. Podobnie, rozkłady normalne mają jeden wspólny wzór, choć nieco bardziej skomplikowany niż ten na funkcję liniową. Widzisz go w górnym lewym rogu poniższej ilustracji:

Rozkład, którego rysunek widzisz, jest jednym z wielu rozkładów normalnych, ale jest to charakterystyczny członek tej rodziny - tzw. rozkład standardowy normalny N(0,1), gdzie zero to pierwszy parametr zwany średnią, a jeden to drugi parametr zwany odchyleniem standardowym.

Wspólny wzór powoduje, że mimo różnic w wyglądzie, członkowie rodziny rozkładów normalnych dzielą podobne własności i to właśnie wykorzystują narzędzia diagnostyczne. Rozsądne byłoby pomyśleć tak: jeśli oczekujemy, aby badana cecha (lub szerzej - zmienna) miała rozkład normalny, to powinna się w rozsądnym stopniu wykazywać tymi właściwościami.

Na przykład, jeśli chcesz sprawdzić, czy masz do czynienia z psem, to sprawdzasz, czy dany obiekt szczeka, ma ogon i chodzi na czterech łapach (lub w odwrotnej kolejności). Wszystkie nieuszkodzone psy mają te właściwości.

NARZĘDZIA DIAGNOSTYCZNE — Narzędzia diagnostyczne dzielą się na liczbowe i na graficzne. Te pierwsze po prostu liczby, a profesjonalnie rzecz mówiąc: statystyki opisowe. Te drugie to wykresy. O ile wskazanie teoretycznych wartości statystyk liczbowych nie jest trudne, problemem staje się to, jak pokazać działanie empirycznych narzędzi na teoretycznym tworze, jakim jest rozkład normalny. Poradzimy sobie, stosując mały trik. Skoro przyjmuje się, że rozkład teoretyczny jakieś cechy to rozkład w całej populacji, to weźmiemy przeogromną próbę i na takiej zbadamy zachowanie narzędzi. W ten sposób będziemy mogli zbliżyć się do teoretycznego rozkładu normalnego i jednocześnie poznać narzędzia diagnostyczne.
Oto lista narzędzi wraz z omówieniem ich zachowania wśród rozkładów teoretycznych (niżej jest lista z omówieniem zachowania w próbie)

• STATYSTYKI OPISOWE
• skośność - miara asymetrii rozkładu. Rozkład normalny ma zerową skośność. Więcej na ten temat znajdziesz w poście: KLIK
  
• kurtoza - miara koncentracji i obecności obserwacji odstających. Rozkład normalny ma zerową kurtozę. Więcej na ten temat znajdziesz w poście: KLIK
• WYKRESY
  
• histogram — wykres pokazujący ogólny kształt rozkładu poprzez zestaw prostokątów, których szerokość to przedział liczbowy, a wysokość to liczba obserwacji, które znalazły się w tym przedziale. Więcej o histogramie: KLIK. Mimo tego, że rozkładu teoretycznego nie przedstawia się za pomocą histogramu, a za pomocą gładkiej linii reprezentującą gęstość lub kropek reprezentujących funkcję prawdopodobieństwa (mówimy o teoretycznych sprawach), to przeogromna próba będzie substytutem populacji. Powinna się wpasowywać w krzywą Gaussa.
  
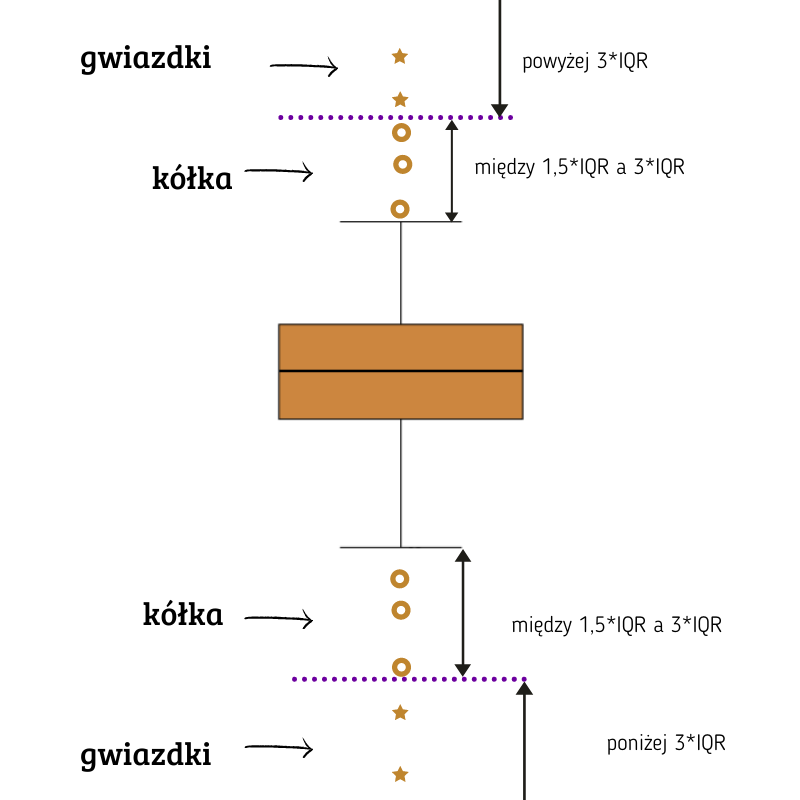
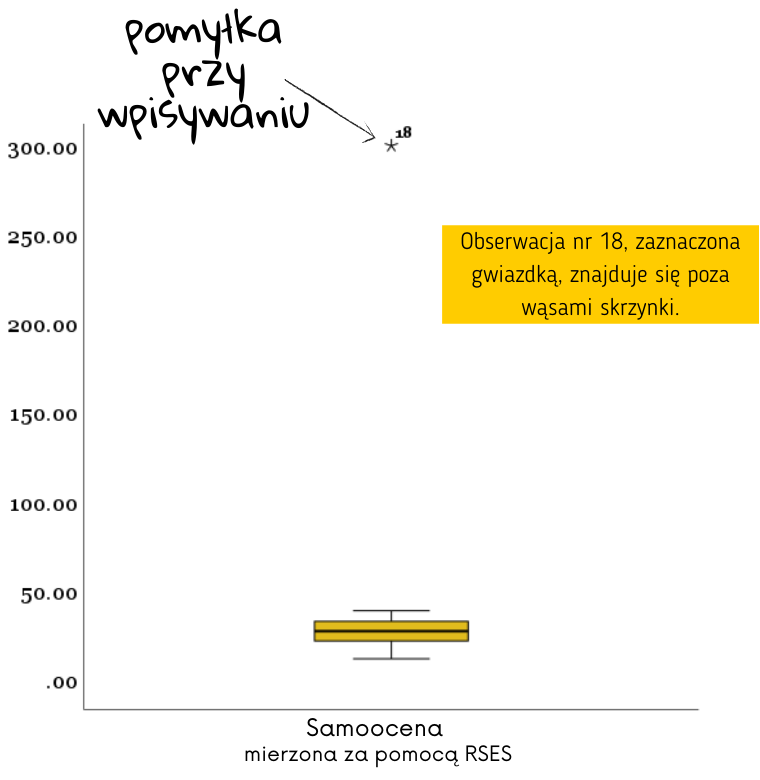
• wykres skrzynkowy (boksplot) - wykres, pokazujący jeden prostokąt z wąsami. Rozkład normalny tworzy wykres postaci:
  
  Jest on symetryczny względem czarnej poziomej linii reprezentującej medianę. Wąsy są w równej odległości od dolnej i górnej krawędzi skrzynki. Rozkład normalny posiada też obserwacje odstające (outliery) - a to ze względu na regułę 3 sigma. Więcej o boxplocie: KLIK
  
• wykres kwantylowy — wykres przestawiający punkty.
  
  Na osiach znajdują się kwantyle rozkładu badanej cechy oraz kwantyle rozkładu normalnego. Więcej o wykresie kwantylowym: KLIK

ZACHOWANIE NARZĘDZI W PRÓBIE — Przeanalizujemy teraz każde z narzędzi i omówimy jego zachowanie w próbie. Przechodząc z teorii do empirii, należy pamiętać, że są dwie rzeczy, które mają wpływ na to, że najczęściej jedno z drugim nie zgadza się i powoduje, że nie możemy oczekiwać tych samych wyników w próbie.

LOSOWA ZMIENNOŚĆ — Wiemy, że rozkład normalny ma zerową skośność i zerową kurtozę, a wykresy mają określony wygląd. Czy w związku z tym możemy oczekiwać, że w próbie będzie dokładnie tak samo? Nie. Te wymagania są zbyt idealne, aby pojawiły się w naszym świecie empirycznym. Rozkład normalny jest przecież rozkładem teoretycznym – zerowa skośność i zerowa kurtoza nie wynika z czyjegoś doświadczenia, a z precyzyjnych matematycznych obliczeń. Trzeba jednak pamiętać, że jest to wynik teoretyczny. Oczekiwania, co do tego, co pojawi się w zebranej przez badacza próbie, muszą być łagodniejsze.

Najłatwiej wytłumaczyć to sobie w następujący sposób: gdybyśmy zgromadzili wszystkie osoby (tj. przebadali całą populację) i wówczas policzyli skośność i kurtozę, to powinna ona wynosić zero - zero jest populacji. Ale próba jest tylko wycinkiem populacji i mogą trafić się różne osoby (czyli wchodzi tu losowość wyników), więc trudno liczyć na to, że skośność i kurtoza będzie równa dokładnie zero. Dlatego musimy wykazać się pewną elastycznością w oczekiwaniu, że wartości statystyk opisowych w próbie będą zero. Innymi słowy, musimy zaakceptować pewne niezerowe (choć bliskie zeru) wartości a nie żądać dokładnych zer.

ZNACZENIE WIELKOŚCI PRÓBY — Trudno jednak nie wspomnieć o wadzie tych reguł kciuka - są one sztywne, czyli niezależne od liczby przebadanych osób. A przecież nawet na chłopski rozum, nawet gdy badana zmienna ma rozkład normalny (np. inteligencja), to wzrost liczby badanych powinien powodować zbliżanie się skośności i kurtozy do tej idealnej, zerowej wartości. Podobnie jest z wykresami. To, co uchodzi w małej próbie, nie powinno przytrafi się w dużej.

REGUŁY KCIUKA — Z pomocą przychodzą wskazówki, które mówią, jaki przedział niezerowych wartości skośności i kurtozy można dopuścić jako przedział takich wartości, które jeszcze nie powodują uznania, że badany rozkład nie jest rozkładem normalnym. Nazywam je regułami kciuka - powinny sprawdzać się w większości typowych sytuacji, ale nie mają statusu twierdzenia matematycznego. Dla ścisłości, będziemy mówić o próbkowej skośności (teoretyczna wynosi 0) i próbkowej kurtozie (teoretyczna wynosi 0) oraz o empirycznych wykresach. Wszystko dlatego, aby podkreślić, że liczymy statystyki i tworzymy wykresu z udziałem próby, a nie teoretycznych wartości.

NARZĘDZIA DIAGNOSTYCZNE

• STATYSTYKI OPISOWE
• skośność — Przedział niezerowych, lecz wciąż akceptowalnych wartości próbkowej skośności to [–1, 1].
  
  
  
  
  
• kurtoza — Przedział niezerowych, lecz wciąż akceptowalnych wartości próbkowej kurtozy jest nieco szerszy niż dla skośności i wynosi [–2,2].
  
  
  
  
  
Jeśli zobaczysz skośność badanej zmiennej w przedziale między minus 1 a 1, to nie odrzucaj od razu normalności rozkładu. Podobnie, jeśli zobaczysz kurtozę badanej zmiennej w przedziale od minus 2 do 2.  To, że skośność wynosi np. 0,56 a nie 0 jeszcze nie oznacza, że rozkład nie może być normalny. Pamiętaj jednak, że ta sama wartość skośności i kurtozy różnie wygląda na tle małej lub dużej próby. Przykładowo, podczas gdy skośność równa 2,01 w próbie liczącej n = 30 osób jest akceptowalna, to w dużej próbie liczącej n = 30 000 osób jest podejrzanie dużym wynikiem.


• WYKRESY
• wykres skrzynkowy (boksplot) — wykres skrzynkowy dla małej próby, N = 10, dla umiarkowanej próby, N = 30, oraz dla dużej próby, N = 1000. Wykres dla dziesięciu osób zupełnie nie przypomina wykresu skrzynkowej rozkładu normalnego, a przecież wiemy, że te dziesięć wartości pochodzi z rozkładu normalnego. Przyczyną jest losowa zmienność, która zaciera charakterystyczną strukturę tego wykresu. Dla trzydziestu wartości boksplot jest przynajmniej symetryczny, a najpiękniejszy z nich jest wówczas, gdy zbierzemy wartości od tysiąca osób.
  
  
• histogram — tutaj również pokazane są histogramy dla trzech typów prób: o bardzo małych liczebnościach, N = 10, dla umiarkowanych prób, N = 30 oraz dla prób o dużej liczebności N = 1000. Histogram rozkładu cechy, nawet jeśli wiadomo, że w populacji jest ona gaussowska, w małej próbie jest w ogólnie podobny do dzwonowej krzywej Gaussa. Cechy charakterystyczne histogramu są widoczne dopiero w dużych próbach.
  
• wykres kwantylowy — aby badana zmienna posiadała rozkład normalny, punkty powinny układać się na prostej. Tak dzieje się na trzecim wykresie, ale jednocześnie jest to wykres próby bardzo licznej o N = 1000 obserwacji. W mniejszym próbach musimy zrezygnować z takiego oczekiwania.
  

KONIECZNOŚĆ STOSOWANIA TESTÓW NORMALNOŚCI? — Narzędzia palpacyjne, takie jak powyżej, to inna oprócz formalnych testów statystycznych metoda badania normalności rozkładu zmiennej. Niestety, badacze są przyzwyczajeni do tego, że testy statystyczne to jedyna poprawna opcja. Tymczasem to po pierwsze nieprawda, jak widać na załączonym obrazku, a po drugie - testy statsytyczne same w sobie obarczone są problemami. Zwróćmy uwagę, że nigdzie nie kontrolujemy liczebności próby, posługując się mglistymi stwierdzeniami, że takie-to-a-taki test jest mocniejszy niż inny. Kierowanie się tylko i wyłącznie istotnością statystyczną testu normalności może sprawić, że badacz popełni błąd. Najlepsze rozwiązanie to łączyć obie metody - palpacyjną i formalną.

DIY - czyli zrób Diagnostykę normalności w SPSS 28. Masz niższą wersję? Nie martw się. Różnice w krokach między tą wersją SPSS a pozostałymi są chyba - nomen omen - nieistotne.

1. Zidentyfikuj zmienną, której normalność chcesz badać. Tutaj ta zmienna nazywa się banalnie - po prostu: Cecha. Następnie wybierz Analiza -> Opis statystyczny -> Eksploracja.

2. Przesuń badaną zmienną z lewego, białego okna na prawe, górne o nazwie Zmienne zależne. Dzięki temu SPSS będzie wiedzieć, którą zmienną diagnozujesz.

Klikając przycisk Statystyki, nic szczególnego nie ma do wyboru. SPSS wie, co ma wybrać. Więc pozostaw zaznaczoną opcję Statystyki opisowe i wciśnij Dalej.

4. Kliknij na drugi od góry przycisk Wykresy. Pojawi się nowe okienko. W panelu Wykresy skrzynkowe pozostaw domyślnie zaznaczoną opcję Poziomy czynnika razem. W panelu Opis odznacz Łodyga-i-liście (tym wykresem nie będziemy zajmować się) i zaznacz Histogram. Następnie, zaznacz okienko Wykresy normalności z testami. Mimo tego, że w tym poście nie zajmujemy się testami normalności, to aby uzyskać wykres kwantylowy (qqplot), musimy zaznaczyć wszystko.

Naciśnij Dalej.

5. Gdy wrócisz do głównego okienka, wybierz OK. To już wszystkie polecenia, jakie są nam potrzebne.

---

PRZYDAŁ SIĘ TEN ARTYKUŁ? LUBISZ TEN BLOG? A MOŻE CHCESZ COŚ ZROBIĆ DLA MNIE? :) Właśnie prowadzę badania nad adaptacją pewnego psychologicznego kwestionariusza. Zbieram odpowiedzi od osób badanych. Ale, nie, nie chcę prosić Cię o wykonanie analiz :) Chcę poprosić Cię o wzięcie udziału i wypełnienie zestawu 49 pytań, które przygotowałam (wraz z moją współpracowniczką, Amelią). Kwestionariusz FoMO dotyczy zjawiska Lęku przed Odłączenie (Fear of missing out, FoMO), czyli lęku przed tym, że inni w tym momencie przeżywają lepsze chwile niż Ty. Skutkuje to byciem przyklejonym do smartfona, skrolowaniem Fejsbuka, sprawdzaniem Messengera, co chwilę, a dalej - poważniejszym problemami niż suchość oczu. Kwestionariusz psychologiczny musi być porządnie przebadanym narzędziem i liczę na to, żę gdy zbiorę i opracuję dane właśnie taki powstanie ze wszystkimi pożądanymi właściwościami, trafnościami, rzetelnościami i innymi homologacjami. TO CO? POMOŻESZ MI? LINK znajdziesz tutaj: KLIK

Wielkość efektu

Mało nam. W statystyce jest już tyle rzeczy - rozmaitego typu testów, wskaźników, mierników. Statystyka sprawia wrażenie gęsto zasiedlonej różnymi bytami - po co więc było tworzyć jeszcze jeden? Wszystko przez tę wstrętną istotność statystyczną, o którą i tak jest sporo nieporozumień. Wbrew pozorom, a wręcz wbrew samej nazwie, istotność statystyczna nie jest tym, czym mogłoby się wydawać. Istotna statystycznie różnica między dwiema grupami wcale jeszcze nie oznacza, że jest ona widoczna gołym okiem i ma znaczenie praktyczne. Maleńka różnica wynosząca np. 1 gram, obsypie się gwiazdkami, gdy wzrośnie liczba obserwacji. Innymi słowami, różnica może być istotna statystycznie, ale nieistotna praktycznie.

Podobny zabieg językowy wykorzystuje się w reklamach. Suplement diety przyczynia się do redukcji wagi. Środek farmaceutyczny wspomaga pracę jelit. Wyrób medyczny redukuje stres i napięcie. Nie wiadomo, jak przyczynia się, na ile wspomaga i jak bardzo redukuje. Już w XIV wieku wiadomo było, że to dawka czyni zarówno lek, jak i truciznę.

NIC NIE JEST TRUCIZNĄ I WSZYSTKO JEST TRUCIZNĄ — Mało rzeczy nie tolerujemy w 0%. Zerowa tolerancja występuje na jeden z pierwiastków - na pluton. Jeśli jakaś substancja występowała w środowisku podczas powstawania naszego gatunku to jest duża szansa, że jakoś ją tolerujemy. Na przykład, jak widzisz, my znosimy tlen wyśmienicie - w przeciwieństwie do bakterii beztlenowych, które wyewoluowały zanim nasz życiodajny pierwiastek rozprzestrzenił się po atmosferze i mogły się do niego przystosować. Dla bakterii beztlenowych tlen jest zabójczy.

Mało rzeczy tolerujemy również w 100%. Mieszanka zwana powietrzem, którą oddychamy nie składa się tylko i wyłącznie z tlenu. Człowiek nie może oddychać czystym tlenem. Za dużo tlenu nie dobrze. Wszystko zależy od dawki.

Istotność statystyczna nie jest istotnością rzeczywistą, a jednak istnieje potrzeba zmierzenia siły zjawiska. Aby móc mierzyć siłę zjawiska i tym samym samym stwierdzenia, czy dawka albo szerzej: różnica między grupami, albo siła korelacji jest wystarczająco duża, aby stwierdzić, że odkryło się coś ważnego. Stąd wymyślono miarę wielkości zjawiska wskaźnik tzw. wielkość efektu (effect size).

DEFINICJA WIELKOŚCI EFEKTU — Jedna z wielu definicji wielkości efektu brzmi: wielkość efektu to ilościowe odzwierciedlenie magnitudy jakiegoś zjawiska, potrzebne do odniesienia się do poruszanego problemu (Kelley, Preacher, 2012). Jest ona bardzo obszerna i obejmuje cały szereg scenariuszy badawczych, co jest i jej wadą, i zaletą. Pokażę więc na przykładzie najprostszego planu badawczego, jak ten wskaźnik działa.

WIELKOŚĆ EFEKTU DLA DWÓCH GRUP — Najprostszy plan badawczy to porównania między dwiema grupami. Na dodatek załóżmy, że są to obserwacje niezależne, to znaczy pierwsza grupa to pewna liczba osób, a druga grupa to ta sama liczba zupełnie innych osób. Innymi słowami, nikt nie został przebadany dwa razy. Osoby badane albo znalazł się w jednej, albo w drugiej grupie. Jedyne co je łączy to to, że badamy je pod względem tej samej cechy. Ta cecha również musi być zgodna z jakimś formatem. Jeśli pamiętasz ze skal pomiarowych Stevensa, to mówię o takiej cesze jest mierzona na skali co najmniej interwałowej (co sprawia, że można policzyć dla niej średnią). Wyniki w większości kwestionariuszy są traktowane jako zmienne interwałowe. W przeciwieństwie do orientacji seksualnej.

Schemat porównań między dwiema grupami wygląda na przykład tak: badanie poziomu otwartości u osób młodych i starszych. Reakcja na bodziec bólowy u osób, którym podano kofeinę i u osób, którym nie podano kofeiny. Nie jest to na przykład: poczucie jakości życia u osób przed i po terapii (osoba badana jest badana dwa razy) albo zależność posiadania kota od płci (dwie zmienne mierzone na skali nominalnej). W analizie danych najczęściej wykorzystuje się test t-Studenta (do chwili, w której piszę te słowa, jest to nadal bardzo popularna sytuacja badawcza). Dla takiego schematu zwanego plan porównań międzygrupowych (albo schemat międzyobiektowy) chcielibyśmy pokazać, jak duża jest różnica między średnimi dwiema grupami.

Przypuśćmy, że badacz chciałby zbadać - poetycko rzecz ujmując - długość dźwięku samotności, czyli to, ile czasu dana osoba może wytrzymać w samotności w pustym pokoju, zanim zacznie szukać towarzystwa - w zależności od tego, czy jest ekstrawertykiem czy introwertykiem. Każda z osób ma swoją długości czasu, którą swobodnie wytrzyma w samotności. Mając dwie grupy, możemy zbadać średni poziom wytrzymałości osobno dla introwertyków i osobno dla ekstrawertyków - po prostu policzmy średnią arytmetyczną. Wiemy już, że średnia arytmetyczna to dobry estymator średniego poziomu zmiennej w populacji KLIK. Dla dwóch grup otrzymamy dwie średnie czasu.

Co dalej? Badacz pracujący w zgodzie z klasyczną statystyką KLIK wykonuje testy istotności statystycznej. Wynik będzie albo istotny albo nieistotny statystycznie, natomiast niezależnie od istotności statystycznej jesteśmy zobligowani do podania tego, jak duża jest różnica miedzy dwiema grupami. Wiemy już też, że sama istotność statystyczna nie przesądza o ważności wyniku.

Można byłoby jedną odjąć od drugiej uzyskując w ten sposób różnica między średnimi w tych grupach i próbować ją oceniać, czy jest duża, czy mała. Jest jednak jeden problem: nawet jeśli istnieją różnice między dwiema grupami, to rozstrzał wyników jest tak duży, że zachodzą one na siebie. Ani introwertycy, ani ekstrawertycy nie są tacy sami. Introwertycy różnią się miedzy sobą pod względem czasu spędzonego samemu ze sobą. Nawet jeśli sama jesteś introwertyczką i możesz dłużej wytrzymać w samotności, to różnisz się pewnie od innego introwertyka, który nie wytrzymuje tak długo.

Niekażdy introwertyk będzie szczęśliwy na kole podbiegunowym i niekażdy ekstrawertyk wybiegnie z pustego pokoju w poszukiwaniu towarzystwa już po sekundzie. Istnieją introwertycy, którzy w samotności wytrzymują krócej niż niektórzy ekstrawertycy. Oczywiście, nie jest to przeważająca większość, introwertyzm zobowiązuje, ale tacy kontr‑introwertycy są. Wniosek jaki z tego płynie jest taki, że i intowertycy, i ekstrawertycy są zróżnicowani w długości wytrzymywania w samotności. Innymi słowami, nie tylko grupy różnią się między sobą, ale w samej grupie występują różnice.

Nie wystarczy zatem odejmować średnie. Musimy zatem coś zrobić, aby okiełznać zróżnicowanie w wynikach wewnątrz tych samych grup. Okazuje się, że dobrym pomysłem jest zmierzyć to zróżnicowanie wewnątrz grup i tym zróżnicowaniem potem podzielić różnicę między średnimi.

Działa to na tej samej zasadzie co wówczas, gdy chcesz się dowiedzieć, czy dużo osób zachorowało na COVID-19 w Irlandii czy w Polsce. Nie interesują Cię bezwzględne, surowe liczby. Na przykład 120 w Irlandii i 150 w Polsce. Na papierze wygląda to tak, jakby w Polsce było więcej. A Polska jest też większa niż Irlandia. Irlandia ma 5 milionów osób. Tyle osób liczy sobie jedno województwo mazowieckie - Polska jest większa niż Irlandia. Wypada zatem uwzględnić różnice w liczbie obywateli. W liczniku mamy liczbę zachorowań, a w mianowniku - populację państwa. Podobnie postępujemy uwzględniając zmienność cechy w dwóch grupach. Dzięki temu przy okazji otrzymujemy tzw. standaryzowaną wielkość efektu. Czyli bezjednostkowy obiekt, który pozwala dokonać porównania.

Mianownik jest jeden, a odchylenia standardowe dwa (po jednym dla każdej z próby). Wobec tego, albo połączymy je albo musimy wybrać.
- możemy pożyczyć odchylenie standardowe od grupy kontrolnej;
- możemy połączyć zmienność dla obu grup i wykorzystać tzw. zmienność połączoną (pooled variance).
Bardzo często stosuje się wówczas d Cohena.

MNOGOŚĆ WIELKOŚCI EFEKTU — Jak widać, wielkości efektu jest bardzo wiele. Są w różnych postaciach nie tylko w obrębie jednego schematu badawczego.

INTERPRETACJA WIELKOŚCI EFEKTU — Dobrze. Wiemy już po co jest wielkość efektu, wiemy że jest wiele rodzajów wielkości efektu, dopasowanych do schematów badawczych (porównania lub korelacje) oraz potrzeb badacza (czy ma porównywać do grupy kontrolnej czy ...). Ale w ostateczności badacz i tak kończy znowu z pojedynczą liczbą, którą teraz musi oceniać pod względem istotności praktycznej.

Założenie jest takie, że kiedy prowadzisz badania w jakiejś dziedzinie, to wiesz, jaka wielkość efektu jest duża. Jeśli np. odchudzasz się, to wiesz, że 1 kg w tydzień to mało, a 5 to dużo, zaś 10 kg to niebezpiecznie dużo. Jeśli prowadzisz badania nad czasem reakcji, to wiesz, czy różnica 5 milisekund jest duża, czy mała. Wiesz to, bo znasz badane zjawisko. Tak wygląda idealna sytuacja, ale psychologia to jednak nie XVIII-wieczna fizyka. Na dodatek często posługujemy się kwestionariuszami samoopisowymi, w których osoby badane umieszczają się na skalach likertowskich.

ROZMIARÓWKA COHENA — Dlatego potrzebna jest nam rozmiarówka. Kiedy naprawdę nie wiesz, czy Twoje d Cohena jest duże lub małe mam dobrą wiadomość - istnieje standardowa rozmiarówka, tak jak w odzieży, która służy do tego, aby ocenić, czy ta wielkość efektu, którą otrzymałaś w badania jest duża, czy mała. Pamiętaj jednak, że jest to tylko ostatnia deska ratunku, gdy naprawdę nie wiesz, jak to zbadać.

WIELKOŚĆ EFEKTU I WIELKOŚĆ PRÓBY — Wielkość efektu można wykorzystać do jeszcze jednej rzeczy oprócz badania ważności wyniku - do wyznaczenia wielkości próby, a po ludzku rzecz ujmując: do odpowiedzi na pytanie, ile osób powinno wziąć udział w badaniu. Robi się to w następujący sposób - pamiętaj, że jesteśmy w świecie klasycznych testów, gdzie mamy błędy I-go i II-go rodzaju oraz spodziewaną wielkość efektu. Te trzy rzeczy musimy wyznaczyć przed zebraniem danych. Zgodnie ze zwyczajem, który mało kto kwestionuje, błąd I-go rodzaju alfa wyznacza się na 5%, a błąd II-go rodzaju beta - na 80%. Zostaje wskazać, jakiej wielkości efektu spodziewamy się. Jest to najtrudniejszy moment. Poza nim zostanie tylko włączyć odpowiednie oprogramowanie, np. G*Power albo R.

Aby posłużyć się jakimś przykładem, musimy sobie wyobrazić konkretny schemat badawczy - to dlatego, że jak już pewnie zauważyłaś, wielkości efektu przychodzą w tylu formach i odmianach, że trudno o bardzo uogólniony przykład.

Powiedzmy, że badamy taką zmienną psychologiczną jak prężność w zależności od tego, czy osoby mieszkają z rodzicami, bądź też nie. Klasyczny schemat porównań między dwiema grupami, stąd odpowiedni będzie d Cohena. Jeśli jesteś wytrawnym badaczem prężności, to wiesz, że można mierzyć to kwestionariuszem KOP-26 lub SPP-25 i to, jak te skale zachowują się, a przede wszystkim, jakie różnice są duże, a jakie małe. To ważne. Inaczej będziesz musiała się wspierać rozmiarówką Cohena. Dla dobra przykładu, tak zrobimy. Wyobraźmy sobie, że spodziewasz się wielkości różnicy między dwiema grupami w prężności d Cohena równej 0,5.

Mamy trzy puzzle: błąd I-go rodzaju, który wynosi 5%; błąd II-go rodzaju, który wynosi 20%; spodziewana wielkość efektu d Cohena, która wynosi 0,5. Czwarty puzzel - liczba osób potrzebnych w badaniu - będzie bonusem. Po wprowadzeniu trzech danych do programu (albo do kalkulatora online) wynosi, że wymagana liczebność wynosi 64 w pojedynczej grupie. Razem potrzebuję zebrać dane od n = 128 osób.

LITERATURA:
Kelley, K., Preacher, K. J. (2012). On effect size. Psychological Methods, 17(2), 137–152. https://doi.org/10.1037/a0028086

Wykres skrzynkowy boksplot

Boksplot to prostokąt z czarną belką w środku oraz na zewnątrz wystającymi antenkami, które nazywa się wąsami (whiskers) - takimi jak u kota. Jest to proste narzędzie do szybkiej oceny Twoich danych. Ponadto pomoże Ci sprawdzić, czy Twoje dane są rozkładu normalnego, czy są obserwacje odstające i może jest jakiś problem z błędami przy wpisywaniu.

SPIS TREŚCI: Co to jest boxplot? Jaka jest jego budowa? Boksplotowe ozdoby - kółka, gwiazdki i co one oznaczają? Detekcja obserwacji odstających za pomocą boksplota Warianty boksplota: pionowa vs. poziomowa Warianty boksplota: sposób tworzenia wąsów Czego nie może boxplot? DIY: Zrób sobie boksplota w SPSS-ie

W boksplotowym prostokącie ważne są: położenie belki względem krótszych boków prostokąta, długość wąsów oraz obecność ozdób. Grubość prostokąta nie jest ważna, więc daje się sterować szerokością rysunku wklejanego do pracy. Na osi pionowej znajduje się skala Twojej zmiennej, więc jeśli jest to wzrost, to zobaczysz tam centymetry (albo metry), a jeśli używasz kwestionariuszy z pytaniami typu Likerta, to powinna być bezjednostkowa skala na przykład od zera do pięciu. Na osi poziomej znajdzie się nazwa Twojej zmiennej.
Wykres skrzynkowy opiera się na trzech kwartylach. Czarna belka prostokąta to mediana (drugi kwartyl Q₂). Górna krawędź to trzeci kwartyl Q₃, zwany też górnym. Dolna krawędź to pierwszy kwartyl Q₁.

Kwartyle są tak wymyślonymi narzędziami statystyki opisowej, że zgodnie z teorią między pierwszym a trzecim kwartylem powinno znaleźć się 50% obserwacji. A więc między górną a dolną krawędzią prostokąta, czyli w skrzynce, jest 50% obserwacji, o których moglibyśmy powiedzieć, że to typowe obserwacje. Gdybyśmy poprzestali tylko na takim kryterium typowości, o tej drugiej połowie obserwacji musielibyśmy powiedzieć, że są nietypowe. To nieco niesprawiedliwe.

Wobec tego, wymyślono rozszerzenie skrzynki, tak aby więcej obserwacji kwalifikowało się jako te typowe. Przy czym zamiast sztucznie rozszerzać skrzynkę, to z góry i z dołu dołączy się antenki (wąsy). Pozostało wówczas pytanie - gdzie te antenki powinny kończyć się? Sztuka polega na tym, aby nie wyrugować ani za mało, ani za dużo obserwacji. I tu przydał się rozstęp międzykwartylowy IQR.

Będziemy iść w górę i w dół od dolnego i górnego kwartyla odmierzając rozstęp międzykwartylowy, IQR, odkładając go odpowiednią liczbę razy. Zgodnie ze sztuką tworzenia boxplotów, powinniśmy oddalić się od górnej krawędzi prostokąta o jeden i pół rozstępu kwartylowego - i tak samo od dolnej krawędzi. Do górnego kwartyla Q₃ dodajemy 1,5 · IQR. Od dolnego kwartyla Q₁ odejmujemy 1,5 · IQR. Tym sposobem mamy zakreślone miejsca, gdzie powinny kończyć się antenki, zwane wąsami.

Ponieważ mediana nie bierze udziału w rysowaniu wąsów, to może znajdować się w dowolnym miejscu wewnątrz i jej umiejscowienie sugeruje to, czy nasz rozkład jest symetryczny, skośny lewo- bądź prawostronnie.

Wybór 1,5 do odmierzania rozstępu międzykwartylowgo IQR od górnej i dolnej krawędzi prostokąta wcale nie jest przypadkowy – za tą liczbą stoi rozkład normalny, co czyni  z boksplota dobre narzędzie do oceny normalności rozkładu Twojej zmiennej.

Przelicznik 1,5 przy odmierzaniu IQR od górnego i dolnego kwartyla czyni z boksplota dobre narzędzie do oceny normalności rozkładu Twojej zmiennej - możesz wizualnie ocenić, czy częstości występowania Twoich obserwacji odzwierciedlają krzywą Gaussa. Boksplot dla zmiennej, której rozkład jest normalny, powinien wyglądać tak:

Co tu widzimy? Mediana znajduje się na środku. Wąsy powinny długość około 1,5ċIQR - jak to sprawdzić? Otóż ten rozstęp międzykwartylowy, IQR, to jest długość ciała skrzynki. Wystarczy więc wizualnie ocenić, czy mniej więcej skrzynka mieści się półtora razy na jednym i na drugim wąsie. Pozostaje pytanie, czy powinny być kółka lub gwiazdki.

KÓŁKA I GWIAZDKI — Na niektórych boksplotach znajdują się ozdoby, w postaci kółek ◦ lub gwiazdek *. Nie są to zwyczajne ozdoby, ale ważne, informacyjne elementy wykresu. Sygnalizują one, które obserwacje znalazły się poza przedziałem wyznaczonym przez wąsy. Takie obserwacje to potencjalne outliery, czyli obserwacje, których wartość różni się znacząco od pozostałych obserwacji. Oczywiście, całe sedno sprawy tkwi, jak bardzo znacząco jest owe znacząco i tutaj trzeba powiedzieć wprost, że nie mamy matematycznej definicji obserwacji odstajacej. Ani też nie mamy jednoznacznego przepisu, co z nimi zrobić. Sam fakt ich wystąpienia nie upoważnia do przyciśnięcia "Delete" w wierszu, w którym się znajdują.

Obserwacja, która znajdzie się poza czubkami wąsów, będzie oznaczona za pomocą symbolu stosowanego przez dany program statystyczny. Najczęściej jest będzie to kółko. W SPSS-ie są to właśnie kółka, ale też gwiazdki.

Część programów różnicuje między te obserwacje, które znajdują się poza wąsami boksplota, ale nie dalej niż o kolejne 1,5 odchylenia standardowego. Czyli te obserwacje, które siedzą między 1,5·IQR a 3 ·IQR to małe outliery, a te które są jeszcze poza trzykrotny rozstęp międzykwartylowy to duże outliery zaznaczone gwiazdką *.

To dlatego, że dla rozkładu normalnego, szansa na znalezienie się 1,5·IQR mniej niż 0,05. A dalej niż 3 · IQR to jeszcze mniej.

Ogólnie panuje przekonanie, że dla rozkładu normalnego nie powinno być żadnych gwiazdek. Otóż prawda jest inna - rozkład normalny ma prawo wygenerować nam kółka i gwiazdki. Przecież jest on określony dla całej osi liczb rzeczywistych: Od minus do plus nieskończoności każda liczba ma prawo wystąpić. Część z nich ma większą szansę wystąpienia, inne zaś bardzo małą, ale wszystkie – niezerową. Aby to zobaczyć, spójrz na poniższy boksplot wygenerowany dla N = 10 000 obserwacji generowanych z rozkładu standardowego normalnego. Ich szansami wystąpienia rządzi rozkład normalny z parametrami μ równym 0 oraz σ równym 1 (czyli rozkład standardowy normalny).

Jak widać, zdarzają się obserwacje odstające. SPSS podaje numer obserwacji, która wypadła poza wąsy - nie pomyl tego z wartością w zmiennej.

DETEKCJA (NIEKTÓRYCH) BŁĘDÓW — Za pomocą boksplota daje radę sprawdzić, czy nie ma błędów przy wpisywaniu wyników. Nie wszystkie omyłkowo wpisane błędy, bo na przykład te, które mieszczą się w skrzynce – takich w których wpisaliśmy za dużą albo za małą wartość. W moim przykładzie użyłam kwestionariusza Rosenberga RSES. To dość stare narzędzie - z lat '60-tych ubiegłego wieku. Służy do zbadania samooceny i składa się z dziesięciu pytań. Można uzyskać od dziesięciu do czterdziestu punktów. W moim przykładzie, badacz omyłkowo wpisał 300 zamiast możliwego 30. Dzięki boksplotowi szybko wykryje ten błąd:

WIELOMODALNOŚĆ ROZKŁADU CECHY — Boksplot to świetne narzędzie, choć ma swoje wady. Wynikają one z tego, że boksplot nie pokazuje kształtu rozkładu w takim stopniu jak histogram. To powoduje, że boksplot jest ślepy na modę. Ogólnie rzecz biorąc, moda to najczęściej występująca wartość. Ta definicja świetnie sprawdza się dla zmiennych jakościowych, natomiast zmienne ilościowe mogą mieć więcej niż jedną modę. Oznacza to, że są co najmniej dwie wartości Twojej cechy, które zdarzają się częściej niż wartości leżące w ich okolicach.

Wzrost człowieka jest dobrym przykładem takiej cechy, po której spodziewalibyśmy się więcej niż jednej mody. Mamy tutaj górkę mniej więcej w okolicach średniego wzrostu kobiet oraz drugą górkę w okolicach średniego wzrostu mężczyzn. Boksplot nie będzie widział tej dwumodalności.

W praktyce prowadzi to do tego, że dwie zmienne różniące się liczbą mód mogą mieć ten sam boksplot.

WARIANTY BOXPLOTA — Do tej pory w tym poście omawialiśmy boksplot po pierwsze: w wersji pionowej, tzn. wartości zmiennej znajdowały się na osi OY oraz po drugie: w wersji z wąsami wyznaczonymi przez rozstęp międzykwartylowy (odkładanie go półtoraza raza od górnej i dolnej krawędzi). Widywane są jednak boksploty w wersji poziomej, gdzie to na osi poziomej OX znajdują się wartości zmiennej. Pod względem budowy, nie różnią się od siebie - to tylko rotacja o 90 stopni.

Widywane są też boksploty, którym inaczej dorysowano wąsy niż poprzez rozstęp międzykwartylowy i taka zmiana konstrukcji ma większe znaczenie niż rotacja. Wąsy można zakreślać przez minimalną i maksymalną wartość cechy.

Taki boksplot jest nadal boksplotem, ale nie pokazuje potencjalnych obserwacji odstających (choć pewnie długość wąsa może dawać do myślenia).
DIY: ZRÓB SOBIE BOXPLOTA W SPSS! — W SPSS-ie są co najmniej dwa sposoby wykonania boksplota. Opisany przeze mnie będzie tym najprostszym, w którym użytkownika interesuje tylko i wyłącznie uzyskanie wykresu.

1. Idziemy: Wykresy ⮚ Wykresy tradycyjne ⮚ Skrzynkowy

2. Pojawia się pierwsze okno dialogowe. Domyślnie jest ustawione, ale my wybieramy drugą opcję. To dlatego, że masz jedną zmienną. Kiedy zaznaczysz ją, wciśnij "Definiuj".

3. Potem musisz przenieść swoją zmienną z lewego, dużego, białego prostokąta do okna z napisem:"Skrzynki przedstawiają". Jak to zrobisz, naciśnij OK na dole tego okna.

4. I to wszystko. W outpucie powinien pokazać się generyczny rysunek boksplota. Pamiętaj, że Twój boksplot będzie wyglądał nieco inaczej. Generyczny, czyli z domyślnymi ustawieniami, a są to: niebieska skrzynka, nazwa zmiennej taka, jak nazwa kolumny, czcionka Sans Serif.

5. Na moich zajęciach ćwiczymy zmysł plastyczny - proszę studentów o to, aby nieco zmodyfikowali wykres, uczynili go przyjemniejszym dla oka. Ustawiamy krój czcionki na Georgia, nazywamy nasze zmienne nieco bardziej po ludzki i zmieniamy kolor skrzynki na jakiś inny (tu pasowało mi żółty). Usunęłam też linie siatki i przeskalowałam wykres, aby był węższy (to akurat proste - łapiesz go z prawej strony lewym przyciskiem myszy i ciągniesz w lewo).

POLECANE POSTY - do przeczytania tego posta dobrze jest mieć opanowane wiadomości z następujących tematów:
Rozkład normalny — post pogłebia wiedzę z rozkładu normalnego
Miary tendencji centralnej — w szczególności o medianie.

Prosto o skośności

SPIS TREŚCI: Co to jest skośność? Przykład: rozkład prawostronnie skośny. Jak wygląda prawostronna skośność na boxplocie? Przykład: rozkład lewostronnie skośny. Jak wygląda lewostronna skośność na boxplocie? Relacja średniej i mediany— czy skośność mówi o tym, że średnia stoi przed medianą? Skośność badanej cechy jako narzędzie diagnostyczne normalności rozkładu Jak powstaje skośność? Efekt podłogi i efekt sufitu

SKOŚNOŚĆ jest pojedynczą liczbą opisującą rozkład, czyli to, jak często zdarzają się wyniki badanej cechy, np. samooceny, narcyzmu, czasu reakcji, wieku, etc. Do tej pory omówiliśmy już kilka pojedynczych liczb informujących o różnych aspektach rozkładu. Są to miary tendencji centralnej, które charakteryzują typową obserwację w próbie, np. średnia, oraz miary stopnia rozproszenia wyników, np. rozstęp albo odchylenie standardowe. Teraz czas na taką miarę, która przekazuje informację o zupełnie innym aspekcie - o tym, czy szanse poszczególnych wartości układają się tak samo po jednej stronie średniej, jak i po drugiej.
W poście o rozkładzie zmiennej losowej jest mowa o częściach jego wykresu: szczycie, ramionach i ogonach:

W rozkładach jednomodalnych (mających jeden garb) i symetrycznych (nie-skośnych) szczyt plasuje się w średniej, np. rozkład normalny i rozkład t-Studenta. Te rozkłady są symetryczne, ponieważ szanse na pojawienie się niższych wartości niż średnia są takie same jak i wyższych. Prosty test na symetryczność polega na złożeniu kartki na pół wzdłuż pomarańczowej linii.

Rozkład jest symetryczny gdy lewa strona rysunku odbije się po prawej stronie.

Nie wszystkie rozkłady są symetryczne. Jeśli w strukturze szans jest jakieś zaburzenie po jednej lub po drugiej stronie średniej, na przykład mamy więcej osób o wyższych wynikach niż o niższych, wówczas rozkład przestaje być symetryczny. Właśnie tę informację przekazuje współczynnik skośności.

ROZKŁAD PRAWOSTRONNIE SKOŚNY — Rozkład jest prawostronnie skośny to rozkład, którego prawy ogon rozkładu jest dłuższy, co oznacza, że mamy dużo obserwacji, które przyjmują wartości mniejsze od średniej. Ze względu na to, że wartość współczynnika skośności w takim przypadku jest wyższa od zera, to taką skośność nazywamy dodatnią.

Przykład: rozkład zmiennej Liczba Urojeń jest rozkładem prawostronnie skośnym w populacji zdrowej. Ogon rozkładu ciągnie się w prawą stronę, a przeważają osoby o liczbie urojeń niższej niż średnia (uwaga: to nie są wyniki konkretnych badań, a jedynie  mnemotechniczna ilustracja zagadnienia).

Skośność można wykryć również oglądając wykres skrzynkowy (boxplot). Jeśli Twoja cecha jest prawostronnie skośna może mieć taki wykres:

ROZKŁAD LEWOSTRONNIE SKOŚNY — Rozkład jest lewostronnie skośny, gdy w próbie przeważają obserwacje o wartościach wyższych niż średnia, a lewy ogon rozkładu jest wydłużony. Ze względu na to, że wartość współczynnika skośności w takim przypadku jest mniejsza od zera, to taką skośność nazywamy ujemną.

Przykład: Rozkład wyników w skali Samooceny mierzonej kwestionariuszem Rosenberga (składającym się z dziesięciu pytań) jest rozkładem lewostronnie skośnym, tak jak ten powyżej. W próbie przeważają osoby o wyższych wynikach samooceny. (Psychologia Społeczna, red. B. Wojciszke (2012)

Jeśli Twoja cecha jest lewostronnie skośna, wówczas wykres skrzynkowy przyjmie taką postać:

RELACJA MIĘDZY ŚREDNIĄ A MEDIANĄ — Jest taka reguła kciuka w książkach ze statystyki, która opowiada o relacji  między miarami tendencji centralnej (średnią i medianą), gdy rozkład jest asymetryczny:
- jeśli rozkład jest prawostronnie skośny, to średnia leży na prawo od mediany (czyli jest większa niż mediana);
- jeśli rozkład jest lewostronnie skośny, to średnia leży na lewo od mediany (czyli jest mniejsza niż mediana) ;
Z grubsza to działa, choć nie zawsze. Skośność nie jest miarą stronności mediany względem średniej.

SKOŚNOŚĆ I NORMALNOŚĆ Jak już mogliśmy przekonać się, skośność przekazuje informację o tym, co dzieje się w zebranych wynikach. Obok tego, ta miara pełni jeszcze jedną ważną funkcję – służy do diagnostyki normalności naszych danych (tzw. rozkładów empirycznych). Rozkład normalny w statystyce klasycznej stanowi bazę dla wielu testów. Aby mogły one zadziałać, żąda się, aby rozkład empiryczny był właśnie takim rozkładem. Licząc skośność, sprawdzamy, czy nasz rozkład jest zbliżony do rozkładu normalnego.

Punktem wyjścia jest fakt, że skośność każdego rozkładu normalnego wynosi zero, 0. W związku z tym, aby nasze dane miały rozkład normalny, muszą mieć również zerową skośność. Tymczasem trudno oczekiwać, żeby skośność w próbie była co do joty zerowa. Ze względu na losowość danych czy błędy pomiarowe, musimy wykazać się pewną elastycznością.

Jedna z reguł o dopuszczalnym zakresie skośności uzyskiwanych przez badacza, mówi, że bezpieczny zakres skośności wynosi [-1,1]. Jeśli obliczona przez Ciebie skośność zawiera się wewnątrz tego przedziału, to możesz uznać, że pod tym względem rozkład Twoich danych jest podobny do rozkładu normalnego.

SKĄD BIERZE SIĘ SKOŚNOŚĆ W DANYCH? — Gdyby przedział możliwych wyników porównać do patyka, to dane mają różne skłonności do obsiadania patyka. Wówczas mogą siedzieć symetrycznie na jego środku, ale mogą też przysiadać na krańcach. Jeśli znaczna część danych siądzie na lewym końcu patyka, to znaczy, że jest bardzo duża koncentracja na wartości minimalnej. Jeśli na prawym krańcu, to na wartości maksymalnej. Pierwszy przypadek nazywa się efektem podłogi (floor effect). Drugi przypadek - efektem sufitu (ceiling effect). Oba mogą przyczynić się do skośności w danych.

EFEKT PODŁOGI (floor effect) — pojawia się wówczas, gdy wyniki w badaniu obsiadają lewy koniec patyka. A więc mamy dużo obserwacji, które przyjęły wartość minimalną, albo prawie minimalną, a mało obserwacji, które są środka przedziału (patyka) lub z jego prawego końca (maksymalna wartość). To się zdarza, gdy badasz populację zdrową pod kątem typowo psychopatologicznych cech, np. psychopatyczności.

EFEKT SUFITU (ceiling effect) — pojawia się wówczas, gdy wynik przekracza możliwości pomiaru narzędzia. Na przykład pacjent ma gorączkę większą niż skala na termometrze rtęciowym, czyli powyżej 43. Termometr nie jest w stanie pokazać dokładnego odczytu, ponieważ prawdziwa wartość znajduje się poza zakresem pomiaru. Choć miernik wskazuje maksymalną wartość, to jeszcze wcale nie oznacza, że nie może być wyżej, a badacz nie wie, jak bardzo wyżej – i bywa, że nie jest to największe zmartwienie.

W serialu Czarnobyl jest scena, w której jeden z bohaterów kwestionuje wskazanie dozymetru - służący do pomiaru dawki promieniowania - mówiąc, że przyrząd ma za mały zakres pomiaru, a prawdziwy wynik jest znacznie wyższy.

Na poniższym rysunku widać wyraźnie efekt sufitu - mogą go zaliczać zbyt łatwe testy. Jeśli w Twoim kwestionariuszu jest za dużo łatwych pozycji (itemów), to możesz po dokonaniu badań zobaczyć taki rysunek.

Miary rozproszenia.

Analizowanie zebranej próby obserwacja po obserwacji byłoby czasochłonne, żmudne, zasobożerne i nieefektywne. Nudne, bezsensowne i jałowe. A i tak ślizgalibyśmy się cały czas po powierzchni. Mam nadzieję, że tym samym jasne stało się dla Was, co czeka badacza który wiersz po wierszu chciałby dowiedzieć się czegoś o badanej cesze w zebranej populacji. Przydałaby się jakaś maszynka, do której włożylibyśmy próbę, a która wyplułaby informację zawartą w próbie - bez konieczności oglądania każdej obserwacji z osobna. Właśnie po to są różne miary, nie tylko tendencji centralnej. Są najczęściej pojedyncze liczby, które agregują informację o cesze z całej próby. Liczby te nazywamy statystykami opisowymi i można je podzielić na cztery grupy - miary tendencji centralnej, miary rozproszenia i miary kształtu. Ten post jest o drugiej grupie - miarach rozproszenia.

W tym poście dowiesz się:
- co to są miary rozproszenia?
- przykład trzech zbiorów o zróżnicowanych miarach rozproszenia?
- rozstęp
- odchylenie standardowe σ oraz wariancja σ²
- po czym nastąpi: ciąg dalszy przykładu
- rozstęp międzykwartylowy
- jak interpretować odchylenie standardowe σ? Przedział typowych wartości
- co to jest współczynnik zmienności?
- na koniec kiedy możesz obliczyć odchylenie standardowe i czy to jest to samo, co błąd standardowy?

---

To nie będzie żart - to ilustracja:
W gabinecie u lekarza.
- Pani wynik badania alfa-beta-gammowego wynosi 17.38.
- Ależ, pani doktor, nic mi to nie mówi...
- No cóż, na szczęście mieści się Pani w typowych wynikach, tj. między 12.34 i 21.43.

Jak widzicie z tego krótkiego przykładu, pojedyncza liczba niewiele mówi o próbie.

---

Są próby, które mają tylko jedną wartość. Na przykład w grupie dwudziestolatków liczącej N=100, wszystkie obserwacje mają w kolumnie (oznaczającej zmienną) „Wiek” wpisaną liczbę „20”. Ale są też takie próby – i te są bardziej interesujące – których wartości zmiennej mają różne wartości. A więc są rozproszone. Dobrze byłoby móc przekazywać taką informację.

---

Miary rozproszenia są to taka grupa parametrów, które "mówią", jak układają się wyniki - najczęściej jak układają się wokół średniej. W psychologii najczęściej spotykane są: odchylenie standardowe/wariancja oraz rozstęp. Inna nazwa, pod jaką funkcjonują, to miary zmienności, ewentualnie miary wariancji (ale to niezręczność językowa).

---

Przykład - trzy zbiory.
Zaczniemy od przykładu. Poniżej wypisałam trzy zbiory. Załóżmy, że są to wyniki kolokwium z pewnego przedmiotu przeprowadzonego w trzech grupach studentów.

A={0,0,0,100,100,100}
B={50,50,50,50,50,50}
C={47,48,49,51,52,53}

Choć średnia w każdym z tych zbiorów wynosi 50, to na pierwszy rzut oka widać, jak bardzo te trzy zbiory różnią się. Aby krótko przekazać informację o rozproszeniu obserwacji, podajemy jedną z miar.

---

Rozstęp.
Jest to po prostu rozpiętość między obserwacjami, a dokładniej różnica pomiędzy wartością największą a najmniejszą. Kolejno w zbiorach z przykładu rozstęp wynosi: 100-0 = 100, 50-50 = 0, 53-47 = 5.
Rozstęp, podobnie jak parametr położenia zwany modą, ma tę zaletę, że łatwo go wyliczyć (trzeba znać jedynie odejmowanie - znacie to? znacie?), ale niestety, traktuje próbę bardzo powierzchownie.

---

Odchylenie standardowe σ oraz wariancja σ².
Te dwa obiekty są w tym samym punkcie ze względu na to, że można jednym ruchem obliczyć odchylenie standardowe, gdy wiadomo, ile wynosi wariancja (i w drugą stronę). Bo:

Odchylenie standardowe σ to pierwiastek z wariancji σ²

...i dobrze byłoby nie rypnąć się w kolejności.

Dalej będę pisać o odchyleniu standardowym, ale to, co napiszę tyczy się w równym stopniu wariancji.

Dużo lepszym od rozstępu, zarówno pod względem własności probabilistycznych, jak i ilości przenoszonej informacji, jest odchylenie standardowe. To akurat musicie uwierzyć mi na słowo, chyba że chcecie krzaczki. Kolejny plus wynika z tego, że przy policzeniu odchylenia standardowego korzystamy ze wszystkich obserwacji w próbie, a nie tylko z wybranych (np. z dwóch jak przy rozstępie).

Tak samo jak w przypadku średniej, korzystanie ze wszystkich obserwacji w próbie niesie ryzyko uwzględnienia obserwacji bardzo nietypowych. Nie ma na to rady, taki jest koszt obliczania odchylenia standardowego.

Wariancji, czyli σ², częściej używają probabiliści. Zaś odchylenie standardowe funkcjonuje dobrze poza matematyką. Głównie z uwagi na to, że wariancja wymaga podnoszenia wartości zmiennej losowej do kwadratu, a co za tym idzie i jednostki, w jakiej wyrażonej jest zmienna. Na przykład: często zmienna Wiek jest wyrażona w latach. Dajmy na to, że średnia wieku studenta to 21 lat, a wariacja wynosi 4 lata kwadratowe. Czery lata kwadratowe! Nie wiem, co to są te lata kwadratowe, ale gdy wyciągnę pierwiastek z 4, to otrzymam szukaną informację: wartość odchylenia standardowego wynosi 2 lata. Posłuży to do obliczenia przedziału typowych wartości (niżej).

---

Ciąg dalszy przykładu.
Wartości odchylenia standardowego σ dla zbiorów A, B i C wynoszą odpowiednio:
- dla zbioru A σ wynosi 1.58;
- dla zbioru B σ wynosi 0 (to dlatego, że nie ma w tym zbiorze żadnego zróżnicowania, wszystkiego obserwacje są takie same)
- dla zbioru C σ wynosi 54.77.
W związku z czym, uzyskaliśmy kolejną, oprócz średniej, informację o tym, jak wygląda próba, bez konieczności analizowania wszystkich obserwacji.

---

Obok odchylenia standardowego σ i rozstępu jest jeszcze:

Rozstęp międzykwartylowy (interquartile range, IQR).
Aby opowiedzieć, czym jest rozstęp międzykwartylowy, należy najpierw powiedzieć, czym są kwartyle.

KwaRtyle... Kwartyle są to takie obserwacje, które dzielą próbę na cztery, w miarę równe, części. Kwartyle, jak sama nazwa ("kwarta") wskazuje, są cztery. Drugi kwartyl już znamy - jest to mediana. Pierwszy kwartyl to "mediana mediany":), czyli połowa pierwszej połowy próby. Trzeci kwartyl to połowa drugiej połowy próby.

Mamy próbę, układamy elementy od najmniejszego do największego i szatkujemy na cztery równe części. Teraz jeśli od trzeciego kwartyla, czyli konkretnej liczby, odejmiemy pierwszy kwartyl, który jest również pewną liczbą, otrzymamy rozpiętość przedziału zawierającego 50% naszej próby i to jest właśnie rozstęp międzykwartylowy.

Przykład. Nasza próba zawiera takie obserwacje: {0,2,4,1,5,6,2}. Po uporządkowaniu wygląda to tak:{0,1,2,2,4,5,6}. Mediana to środkowa obserwacja, czyli "2". Pierwszy kwartyl to mediana pierwszej połowy, czyli 1. Trzeci kwartyl to mediana drugiej połowy czyli 5. Stąd IQR wynosi 5-1 = 4, słownie:"cztery". Oczywiście, SPSS lub R za nas kalkuluje te wartości.

Serio, zawsze się zastanawiam, czy jest sens zadań rachunkowych na zajęciach ze statystyki. Jeśli masz jakieś z tym przemyślenia, to proszę podziel się ze mną (w komentarzu, albo przez formularz).

---

Jak interpretować odchylenie standardowe σ? Przedział typowych wartości.

Wartość średnia x̄ podaje, gdzie mniej więcej znajduje się centrum próby. To już wiemy. Natomiast odchylenie standardowe σ opisuje, jak obserwacje układają się wokół tego centrum. Jeśli ktoś mówi, że zmienna Wiek ma średnią 23.5 oraz odchylenie standardowe 1.5, to znaczy, że typowe pod względem zmiennej Wiek obserwacje może znaleźć w przedziale [23.5-1.5. 23+1.5], co daje wynik: [22,25].

---

Czasami, choć ja jeszcze nie spotkałam się z tym wykonuje się porównanie zmienności w dwóch grupach badanych. Używany jest wtedy:

Współczynnik zmienności, coefficient of variantion (CV).

Aby poradzić sobie z oceną wielkości miary rozproszenia w dwóch grupach badanych (np. eksperymentalna i kontrolna, lub: kobiety i mężczyźni), możemy posłużyć się współczynnikiem wariancji, który jest stosunkiem odchylenia standardowego do średniej.

Tak, jak już napisałam wyżej, jakoś nie zauważyłam specjalnej popularności tego współczynnika w populacji psychologów, ale dobrze wiedzieć, że coś takiego istnieje.

Największy sens, gdy skala jest przedziałowa. Przykład – to są hipotetyczne wyniki: Średni poziom na skali Nieśmiałości wśród kobiet wynosi 21.85, a odchylenie standardowe jest 6.88. Z kolei wśród mężczyzn, średni poziom na skali Nieśmiałości wynosi 24.39 z odchyleniem standardowym 8.18.
Jak porównać te wyniki? Właśnie za pomocą współczynnik zmienności (najwygodniej te współczynniki podać w procentach).

W grupie kobiet wynosi 0.31, czyli 31%, w grupie mężczyzn 0.34, więc 34%. Wniosek, jak widać, większe (choć nieznacznie większe) zróżnicowanie jest wśród mężczyzn niż wśród kobiet.

---

A jeśli mamy więcej niż jedną zmienną?
W przypadku większej ilości zmiennych, o miarach współzależności poczytaj tutaj: KLIK

---

Pamiętaj!
- To, czy możesz obliczyć odchylenie standardowe zależy od typu skali pomiarowej. Dla zmiennej „Płeć” nie ma sensu obliczać wariancji, nawet jeśli w kolumnie jest ciąg zer i jedynek.

- Być może już słyszałaś o czymś takim jak błąd standardowy. Otóż, błąd standardowy to coś innego niż odchylenie standardowe. Najprostsza różnica między nimi jest taka: błąd standardowy odnosi się do estymatora a odchylenie standardowe z próby odnosi się do ... próby. To tak w dużym skrócie i tylko po to, aby nie traktować tych pojęć jako synonimy.

---

Cześć! Dzięki za przeczytanie mojego posta. Przy okazji, mam do Ciebie małą prośbę - siedzę tu, po drugiej stronie monitora i nie widzę, czy podobała Ci się treść artykułu, czy może znużyła, może jest tego za dużo, albo było za długie (opcja TLDR, czyli Too Long Didn't Read). Przygotowałam kilka możliwych reakcji, spójrz niżej - proszę, podziel się swoimi odczuciami, ponieważ nie mam okazji bezpośrednio Ciebie zapytać, a jestem bardzo ciekawa. Przyda mi się to do planowania i pisania kolejnych postów. Jeszcze raz dzięki za uwagę i do zobaczenia :-)

Miary tendencji centralnej (średnia, mediana, moda).

Analizowanie zebranej próby obserwacja po obserwacji byłoby czasochłonne, żmudne, zasobożerne i nieefektywne. Nudne, bezsensowne i jałowe. A i tak ślizgalibyśmy się cały czas po powierzchni. Mam nadzieję, że tym samym jasne stało się dla Was, co czeka badacza który wiersz po wierszu chciałby dowiedzieć się czegoś o badanej cesze w zebranej populacji. Przydałaby się jakaś maszynka, do której włożylibyśmy próbę, a która wyplułaby informację zawartą w próbie - bez konieczności oglądania każdej obserwacji z osobna. Właśnie po to są różne miary, nie tylko tendencji centralnej. Są najczęściej pojedyncze liczby, które agregują informację o cesze z całej próby. Liczby te nazywamy statystykami opisowymi i można je podzielić na cztery grupy - miary tendencji centralnej, miary rozproszenia i miary kształtu. Ten post jest o tej pierwszej grupie - miarach tendencji centralnej.

Tendencja centralna skupia się na scharakteryzowaniu typowego egzemplarza w danych. 

Przykład - kiedy prababcia pyta Cię, co to jest hipster, to opiszesz jej typowego hipstera. Powiedz to jest ktoś, kto ubiera się w spodnie-rurki i mądre koszulki, ma brodę (mężczyźni) i wielkie okulary. I generalnie jest na nie, kiedy większość jest na tak. Generalnie, babciu, są to młodzi, bogaci z dobrych rodzin, mieszkający na amerykańskich przedmieściach.

Tak działa tendencja centralna - chodzi o wczucie się w próbę. A profesjonalnie mówiąc, chodzi o środek ciężkości próby. Miary tendencji centralnej odpowiadają na pytanie: jaki jest typowy egzemplarz. Mamy wiele sposobów, aby skonsumować to pytanie - najpopularniejsze trzy z nich to: moda, mediana i średnia.

---

Moda

Moda ma wiele nazw: dominanta, wartość dominująca, modalna, wartość modalna. Najprostsza definicja mody brzmi: najczęściej występująca wartość.

Definicja ta idealnie sprawdza się dla zmiennych nominalnych, typu: płeć (jaka płeć przeważa w próbie?), wyznanie (o jakiej najczęściej religii są osoby z próby) czy fakt przeżycia (w mojej próbie więcej osób przeżyło niż nieprzeżyło).

Ta statystyka, zwana modą, może przyjmować wartości liczbowe i tekstowe. To niekoniecznie musi być "kobieta", "buddysta" i "żyje". To może być "średnie", 34,56 oraz pi i pół. W przypadku zmiennej nominalnej moda oznacza najczęściej występującą wartość i jeśli są dwie wartości np. "katolicy" i "buddyści", którzy występują tyle samo razy, to mamy dwie mody. Jeśli wszystkie wartości zmiennej występują tyle samo razy, to masz dwa wyjścia: albo uznać, że wszystkie wartości są modami (to nie czyni Twojej próby wyjątkową) albo żadna (to również nie czyni Twojej próby wyjątkową).

Nieco inaczej jest dla zmiennych mierzonych na skali mocniejszej niż nominalna. Zobaczmy dla skali porządkowej. Zmienną jest dochód w rodzinie podzielony na trzy kategorie: niewielki dochód, średni dochód i duży dochód.

Wykres słupkowy liczebności zmiennej Dochód w pewnej próbie (Rys. LJK)

Kategorie niski i duży dochód mają taką samą liczebność (n = 35). Najmniej osób określiło swój dochód jako średni. Mamy tutaj dwie mody, bo dwie wartości występują jednakowo często: to jest niski i duży dochód.

A teraz spójrzmy jeszcze raz. Tutaj mamy dużo osób, które dochód określiło jako niski (n=55), nieco mniej (n=35) mamy osób, które określiło dochód jako duży (n=35). Ile mód mamy?

Wykres słupkowy liczebności zmiennej Dochód w pewnej próbie (Rys. LJK)

Mamy dwie mody. Dlaczego? Przecież dla zmiennej nominalnej to byłaby jedna - niski dochód. Ale tutaj mamy dwie - bo są dwie górki.

Na powyższym przykładzie widać inne traktowanie mody dla zmiennych nominalnych i dla całej reszty. To wynika z tego, że moda tak naprawdę oznacza liczebną dominację jednej wartości nad pozostałymi - w pewnym lokalnym otoczeniu. Lokalnym otoczeniem dla obu wartości: niski dochód i duży dochód jest wartość średni dochód, która mniej liczna.

Tworzy to charakterystyczną górkę w liczebnościach. To jest właśnie istota pojęcia moda: wystarczy zdominować sąsiadów, aby być modą. Jeszcze lepiej niż dla zmiennej porządkowej widać to dla zmiennych interwałowych, o ilorazowych już nie wspominając. Zobaczcie - weźmy zmienną ilorazową Waga.

LJK

Tutaj mamy dwie górki - dwie mody. Inaczej niż w przypadku zmiennej nominanej i jej wykresu słupkowego, te górki nie muszą być tej samej wysokości. Ważne, aby były górkami.

To wszystko prowadzi nas do jednego interesującego wniosku: moda jest nie tylko miarą tendencji centralnej, ale także pewną miarą kształtu - ilości górek. Powyżej widać rozkład bimodalny (dwumodalny). Mogą być też rozkłady wielomodalne - o większej ilości mód.

Co to wszystko znaczy? Liczba mód bywa bardzo ważnym źródłem informacji dla badacza. Cecha, która ma dwie mody, to cecha, która ma dwie grupy obserwacji: jedne siedzące w pierwszej górce, drugie siedzące w drugiej górce. Bywa, że fakt bimodalności świadczy o tym, że różne mechanizmy leżą u podłoża zjawiska. Popatrz niżej na przykład z zapadalnością na schizofrenię.

Zależność zapadalności na schizofrenię od wieku (Rys. LJK).

Tak właśnie było z zapadalnością na schizofrenię. Początkowo badacze widzieli, że są dwie mody w wieku zapadania na schizofrenię. Potem jednak okazało się, że przyczyną tego zjawiska jest to, że bardzo duże znaczenie ma płeć. Kobiety zapadają później, a mężczyźni - wcześniej.

Tak działa moda. Niby taka prosta sprawa, ale może przekazać ważne informacje.

---

Mediana
Najprościej rzecz ujmując, mediana to taki punkt, który dzieli próbę na pół. Połowa obserwacji jest niemniejsza, a połowa obserwacji jest niewiększa.

Aby wyznaczyć medianę, należy najpierw uporządkować próbę pod względem badanej cechy w kolejności od najmniejszej do największej. Z tego wynika, że wypadają nam wszystkie zmienne mierzone na skali nominalnej. Nie da się uporządkować zmiennej takiej jak Wyznanie, Płeć czy Status przeżycia. Ale da się ze zmiennymi, mierzonymi na wyższych poziomach.

Podczas porządkowania mentalnie numerujemy każdą obserwacji w rządku. Profesjonalnie nazywa się to rangowaniem: pierwsza, druga, trzecia... 

Kiedy już uporządkujemy obserwacje, wybieramy środek.

Najłatwiej jest gdy masz nieparzystą liczbę obserwacji w próbie (przebadałaś 5 osób), to wówczas bierzez po prostu środkową obserwację. Jeśli masz parzystą liczbę obserwacji (przebadałaś 10 osób albo 22 osoby, albo 7138 <- daj-ci-boże, jak mawiała moja babcia), to wówczas należy wziąć połowę między środkowymi wartościami.

Np. w próbie mamy obserwacje o wartościach: 4, 7,4, 5,1,4. Po uporządkowaniu jest to 1,4,4,5,7.

Jeśli dołożymy jeszcze jedną obserwacją - o wartości 12, wówczas w uporządkowanej już próbie będziemy mieć: 1,4,4,5,7,12. Środkowe są dwie: 4 i 5. Więc trzeba wziąć obserwacje z środka: obserwację trzecią oraz obserwację czwartą, zsumować i podzielić. W ten sposób mamy 4+5=10, 10:2 = 4.5. Uważaj, aby się nie pomylić w tym.

No, a teraz problemy z liczeniem mediany. I tak jak w przypadku mody, najsłabsza skala, na której można było wykonać czynność obliczania danej statystyki, miała swoje kruczki. Tutaj wiemy, że najsłabszą skalą jest skala porządkowa.

Założmy, że mamy próbę: podstawowe, podstawowe, średnie, wyższe, wyższe. Uporządkowałam je już rosnąco. Kiedy już wiemy kto stoi za kim, to sięgamy po wartość środkową. Jeśli przebadaliśmy niepatrzystą liczbę osób, to środek jest jeden. W moim przypadku jest to liczba 3 odpowiadająca średniemu wykształceniu.

W przypadku, gdy obserwacji jest parzysta liczba, to wówczas mamy mały problem, bo nie da rady policzyć połowy. Powiedzmy, że mamy: podstawowe, podstawowe, średnie, wyższe, wyższe, wyższe.

Dołożyłam jedną osobę o wyższym wykształceniu. Teraz trzecią obserwacją jest średnie, a czwartą jest wyższe. No i jak z tego zrobić średnie i pół? Na ich rangach da się to zrobić: (3+4)/2=3.5 Ale nie na ich wartościach. Wobec tego w takich przypadkach możesz podać dolną medianę (średnie), albo obie (średnie i wyższe). To powinno załatwić sprawę, ale pokazuje, jak niewygodne jest liczenie czegokolwiek na zmiennych, które są porządkowe.

---

Średnia.

Średnia jest przeciwieństwem mody, jeśli chodzi o stopień wgłębienia się w próbę. O ile moda korzysta z paru obserwacji, to średnia - ze wszystkich na raz. Oczywiście, nie w takim samym stopniu - raczej waży każdą z wartości poprzez to, ile razy wystąpiła.

Średnich jest wiele: arytmetyczna, harmoniczna, geometryczna (i jeszcze kilka). To od dziedziny zależy, która średnia będzie najczęściej używana. W psychologii jest to średnia arytmetyczna. Działa w ten sposób, że najpier lepi obserwacje w całość (to jest w liczniku) i rozdając na nowo każdemu po równo (to jest to, co się dzieje w mianowniku).

Średnia artymetyczna ma bardzo dobre właściwości matematyczne - poza tym, że korzysta z każdej pojedynczej obserwacji.

O tym dlaczego średnia arytmetyczna jest dobrym oszacowaniem prawdziwej wartości parametru w populacji możesz poczytać w poście o estymatorach.

Problemem średniej jest to, że jest wrażliwa na tzw. obserwacje odstające (outliery).

W skrócie: są obserwacje, które mają stosunkowo dużą wartość w porównaniu do całej reszty. Przykładowo ktoś, kto jest bardzo wysoki - zawodowy koszykarz - jest w grupie przedszkolaków obserwacją odstającą. 

Gdybyśmy policzyli średnią arytmetyczną wzrostu grupy przedszkolaków, a potem policzyli średnią wzrostu grupy przedszkolaków wzbogaconej koszykarza, okazałoby się że jego wzrost zniekształca wartość średniej.

(112+115+109)/3=112 cm (przedszkolak)

(112+115+109+224)/4=140 cm (wczesny nastolatek)

140 cm to dużo jak na przedszkolaka. Koszykarz bardzo podbił średnią wzrostu dzieci.

Wszystkie trzy miary badają typowy egzemplarz. Ale każda z nich robi to na własny sposób, co wiąże się zarówno z zaletami, jak i z ograniczeniami. Podsumujmy zady i walety miar tendencji centralnej.

---

Statystyka	Minusy	Plusy	Skale
Moda	nie korzysta z całej próby	odporna na obserwacje odstające	nominalna, porządkowa, interwałowa, ilorazowa
Mediana		odporna na obserwacje odstające	porządkowa, interwałowa, ilorazowa
Średnia	wrażliwa na obserwacje odstające	korzysta z całej próby	interwałowa, ilorazowa

---

Co to znaczy mieć średnio dwa i pół przyjaciela: zmienne dyskretne a ciągłe.

Liczba przyjaciół jest zmienną mierzoną na skali ilorazowej. Można mieć jednego przyjaciela, można mieć pięć razy więcej przyjaciół, czyli pięć. 

Powiedzenie mam dwa razy więcej przyjaciół niż John ma sens. Co więcej, zero w tej zmiennej Liczba przyjaciół również ma sens, ponieważ można mieć zero przyjaciół. Nie można zejść poniżej zera - nikt nie ma minusowej liczby przyjaciół. Tego nawet nie da się opowiedzieć, co miałoby to znaczyć.

Może okazać się, że w Twojej próbie średnia liczba przyjaciół wynosi 2.76. Ale nikt nie ma dwa i siedziemdziesiąt sześć setnych przyjaciela. To nie ma sensu - pomyślisz - czy coś tu jest nie tak? Nie. To jest normalne zjawisko, które dotyczy zmiennych dyskretnych i obliczania średniej. Zmienne dyskretne to są takie zmienne, których wartości są izolowane od siebie. Liczba przyjaciół jest świetnym przykładem, ponieważ między wartość: jeden przyjaciel a dwóch przyjaciół nie ma półtora przyjaciela.

Między dwie sąsiadujące wartości nie rady wcisnąć trzeciej tak jak w przypadku takich zmiennych jak waga, wzrost, wiek, czas, długość łokcia. Tutaj zawsze między 23,56 cm a 23,57 można wcisnąć 23,565 - i cały przedział innych. Takie zmienne, które maą wartości w przedziałach, nazywane są zmiennymi ciągłymi.

Jak to się ma liczenia średniej? Chodzi o sensowność, o interpretacją wyniku. Fakt, że wartość średniej w Twojej próbie nie ma namacalnego znaczenia nie dyskwalifikuje samej zmiennej w skali pomiarowej. Liczba przyjaciół nadal jest zmienną ilorazową. Ale po prostu wybierz inną miarę tendencji centralnej, zwłaszcza gdy prezentujesz wyniki osobom spoza dziedziny. W przykładzie z liczbą przyjaciół lepszą miarą byłaby moda: w Twojej próbie najczęściej ludzie mają troje przyjaciół.

---

Kiedy mam zastosować średnią a kiedy modę lub medianę?

Po pierwsze: cel badania. Po drugie: skala pomiarowa zmiennej. Po trzecie: kształt rozkładu. Dużo zależy od innej statystyki - od skośności. Spójrz na wykres częstości (histogram), na rozkład wartości Twojej cechy. Jeśli Twoje dane są symetryczne, wówczas możesz wziąć średnią. Ale jeśli jedno z ramion rozkładu jest wyciągnięte w którąś ze stron, wówczas średnia może nie być najlepszą miarą, więc wybierz medianę.

Rys. Prawostronna skośność Czasu reakcji i to, jak daleko od siebie leżą średnia i mediana (Rys. LJK).

Średnia zjechała bardzo w prawo. W takim przypadku lepiej podawać medianę.

Nawet na zdrowy rozsądek to ma sens. Wyobraź sobie, że idziesz do firmy. 99% pracowników zarabia bardzo mało, a 1% zarabia bardzo dużo. Jeśli zapytasz o średnią i na tej podstawie dokonasz wyboru, to wprawdzie statystyka będzie dobrze policzona, ale Twój entuzjazm będzie nadmierny. Lepiej pytać o medianę, bo wówczas wartości odstajace będą zepchnięte albo na początek, albo na koniec kolejki i uzyskasz wartościową informację.

Jest jeszcze po czwarte: nasza psychologiczna biblia edytorska. To, jak ma wyglądać artykuł naukowy w psychologii, jest dokładnie opisane w Manualu APA, czyli podręczniku publikacyjnym Amerykańskiego Towarzystwa Psychologicznego. Czcionka, wielkość i jej krój, wygląd strony tytułowej, czy pisać "upośledzeni umysłowo" czy "osoby z upośledzeniem umysłowym"? Wszystkie to znajdziesz w tej książce. Rządzi ona również regułami opisu statystycznego, dlatego podstawowym zestawem statystyk jest średnia artymetyczna oraz odchylenie standardowe.

---

Miary tendencji centralnej to za mało...
Z poprzedniego akapitu wynika, że sama średnia, czy inna miara tendencji centralnej to trochę mało, aby wyrobić sobie zdanie o próbie. Zobacz przykład.

Poniżej wypisałam trzy zbiory. Są to moje ulubione zbiory do pokazywania zasad działania różnych parametrów. Dla wygody, załóżmy, że są to wyniki kolokwium z pewnego przedmiotu przeprowadzonego w trzech grupach studentów.

• A=0,0,0,100,100,100
• B=50,50,50,50,50,50
• C=47,48,49,51,52,53

Średnia Średnia w zbiorze A wynosi 50, ponieważ 0 + 0 + 0 + 100 + 100 + 100 = 300. Liczba elementów w zbiorze A wynosi 6, stąd 300 : 6 = 50. Mówi się, że 0 to tyle, co nic, ale należy zera traktować jako normalne, pełnoprawne obserwacje, które po prostu przyjmują wartość ‘zero’. Czy to jest tutaj dobra miara? Nie, bo tak naprawdę mamy tylko dwie skrajne wartości cechy występujące trzykrotnie. Średnia w zbiorze B i C również wynosi 50.

Mediana Mediana w zbiorze A wynosi 50, ponieważ mamy dwie “środkowe obserwacje”, zatem biorę ich średnią arytmetyczną (0+100)/2=50. Mediana w zbiorze B wynosi (50+50)/2 = 50. Mediana w zbiorze C wynosi (49+51)/2=50. Wszystkie trzy zbiory mają tę samą średnią i medianę.

Moda Moda w zbiorze A albo nie istnieje, albo jest ich dwie - 0 i 100, ponieważ występują tyle samo razy. Moda w zbiorze B jest bardzo widoczna i wynosi 50. Moda w zbiorze C nie występuje, ponieważ każda wartość występuje tylko raz.

Trzy zbiory, ta sama średnia, a tak bardzo różnią się.

---

Jak widać, można się oszukać, gdy się patrzy tylko i wyłącznie na środek ciężkości próby. To dlatego warto też przyjrzeć się innym miarom, już nie tendencji centralnej, ale choćby miarom rozproszenia.

---

Cześć! Dzięki za przeczytanie mojego posta. Przy okazji, mam do Ciebie małą prośbę - siedzę tu, po drugiej stronie monitora i nie widzę, czy podobała Ci się treść artykułu, czy może znużyła, może jest tego za dużo, albo było za długie (Too Long Didn't Read, TLDR). Przygotowałam kilka możliwych reakcji - proszę, podziel się swoimi odczuciami, ponieważ nie mam okazji bezpośrednio Ciebie zapytać, a jestem bardzo ciekawa. Przyda mi się to do planowania i pisania kolejnych postów. Jeszcze raz dzięki za uwagę i do zobaczenia :-)